Wie kommt auf die 3.0625 oder generell auf so ein Ergebnis?

Question

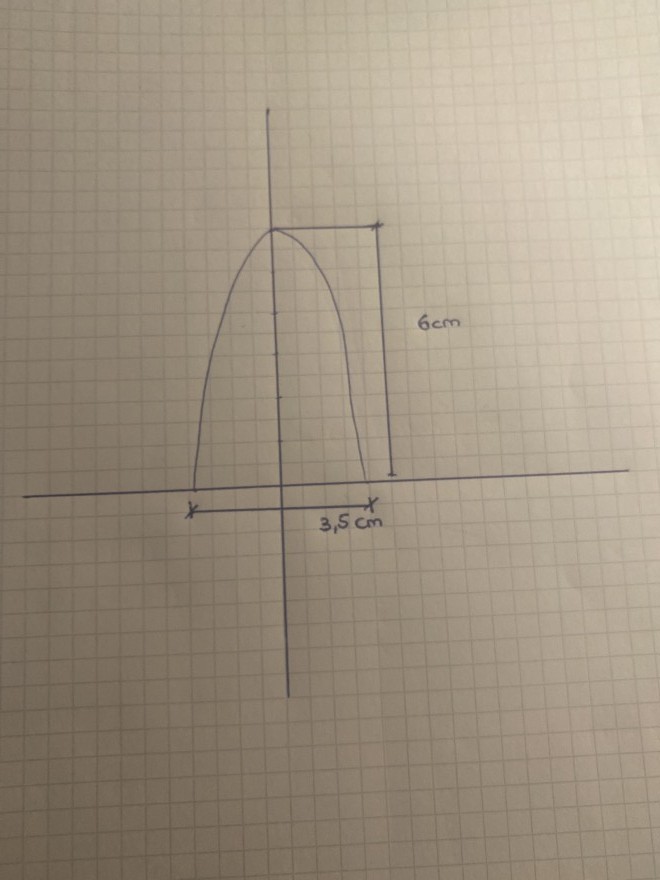
Der Querschnitt eines Salzstreuers hat die Form einer Parabel. Gib die zugehörigen Parabelgleichung an.

Problem/Ansatz:

Wir haben das heute besprochen. Aber ich versteh des trotzdem nicht. Die Lösung wäre :

y= - 6/ 3.0625cm^-1 • x^2 + 6 cm

Wie kommt auf die 3.0625 oder generell auf so ein Ergebnis ?

Ich würde mich sehr über eine Erklärung freuen. :)

Answer 1

Bei x = 1,75 ( die Hälfte von 3,5 ) wäre x^2 gleich 3,0625, die Parabel soll da aber den Wert 6 haben und nach unten gebogen sein, darum -6/3,0625 , da f(0) = 6 sein soll.

Dann noch plus 6

$$f(x)=-6/1,75^2*x^2+6$$

$$f(x)=-6/3,0625*x^2+6$$

Answer 2

Ansatz (wegen der Nullstellen: y=a·(x-1,75)·(x+1,75). Den Punkt (0|6) einsetzen ergibt a=-96/49. Ergebnis: Die Parabelgleichung lautet: y=-96/49·(x-3.5)·(x+3.5) oder nach Ausmultiplizieren y=6-96/49·x².

Answer 3

( x | y )
( 0 | 6 )
( 1.75 | 0 )

y = a*x^2 + b

y = a*0^2 + b = 6
b = 6 ( y-Achsenabschnitt, auch aus der Skizze ablesbar )

y = a * x^2 + 6
0 = a * (1.75) ^2 + 6
a = - 1.96

y = - 1.96 * x^2 + b