Von einem Polynom f(x) unbekannten Grades ist folgende Wertetabelle bekannt:
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| f(x) | 0 | 8 | 54 | 192 | 500 | 1080 | 2028 |
Dann kann man den Graphen des Polynoms angenähert durch einen Polygonzug darstellen:
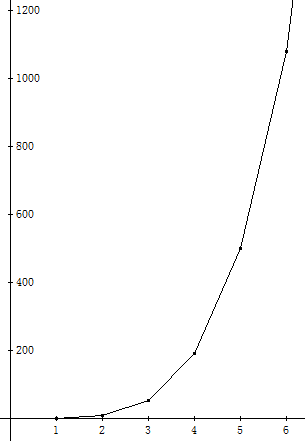
Auch eine Folge von Steigungswerten des unbekannten Polynoms lässt sich angeben: [8, 46, 138, 308, 580, 978]. Die Stellen, an denen diese Steigungen angenommen werden, lassen sich abschätzen. Generell schätzen wir, dass die durchschnittliche Steigung einer Kurve über einem Intervall etwa in der Mitte des Intervalls von der Kurve selbst angenommen wird. Die ungefähre Wertetabelle der ersten Ableitung sieht dann so aus:
Wert der Stelle
| 1,5 | 2,5 | 3,5 | 4,5 | 5,5 | 6,5 |
Wert der Steigung an dieser Stelle
| 8 | 46 | 138 | 308 | 580 | 978 |
Der Graph der ersten Ableitung kann dann durch einen Polygonzug angenähert dargestellt werden:
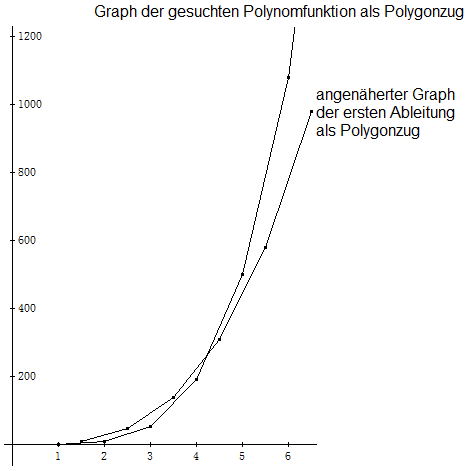
Mit Hilfe der soeben genannten Wertetabelle der angenäherten ersten Ableitung kann eine Wertefolge der zweiten Ableitung abgeschätzt werden: [38, 92, 170, 272, 398]. Die Stellen, an denen die zweite Ableitung diese Werte annimmt, schätzen wir ebenfalls ab und erhalten eine grobe Annäherung an eine Wertetabelle der zweiten Ableitung:
Geschätzte Stellen der Werte von f ''
| 2 | 3 | 4 | 5 | 6 |
Werte der zweiten Ableitung
| 38 | 92 | 170 | 272 | 398 |
Auch zu dieser Wertetabelle zeichnen wir den Polygonzug, der den Graphen der zweiten Ableitung vermutlich gut annähert:
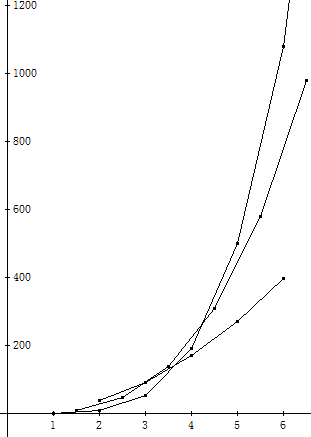
Die Wertefolgen aus den drei bisher genannten Wertetabellen sind
[0, 8, 54, 192, 500, 1080, 2058]
d1= [8, 46, 138, 308, 580, 978]
d2= [38, 92, 170, 272, 398].
Dabei sind d1 und d2 jeweils die Differenzenfolgen der vorausgegangenen Wertefolgen. Wir nennen sie die erste und die zweite Differenzenfolge der durch ihre ersten Glieder gegeben Ausgangsfolge. Wir erinnern uns, dass wir den Grad des zugehörigen Polynoms suchen. Wir bilden noch die dritte und die vierte Differenzenfolge:
d3= [54, 78, 102, 126]
d4= [24, 24, 24].
Damit kennen wir die ungefähren Wertetabellen der dritten und der vierten Ableitung:
Geschätzte Stellen der Werte der dritten Abl.
| 2,5 | 3,5 | 4,5 | 5,5 |
Werte der dritten Ableitung
| 54 | 78 | 102 | 126 |
und
Geschätzte Stellen der Werte der vierten Ableitung
| 3 | 4 | 5 |
|
Werte der vierten Ableitung
| 24 | 24 | 24 |
|
Die Graphen der dritten und der vierten Differenzenfolgen sind Geraden. Sie nähern die Graphen der dritten und der vierten Ableitung an. Es liegt nahe zu vermuten, dass der exakte Graph der dritten Ableitung parallel zu dem durch die Wertetabelle abgeschätzten verläuft. Der Graph der vierten Ableitung könnte sogar exakt sein.
Nehmen wir also an, dass die vierte Ableitung konstant ist und das gesuchte Polynom folglich den Grad 4 hat. Nun können wir in den Ansatz f(x)=ax4+bx3+cx2+dx+e fünf Punkte aus der gegebenen Wertetabelle einsetzen und erhalten fünf Gleichungen mit fünf Unbekannten und daraus die Lösungen a=1, b=-1, c=0, d=0 und e=0. Wenn wir das so gewonnene Polynom f(x)=x4-x3 mit der eingangs gegebenen Wertetabelle vergleichen, stellen wir fest, dass wir das gesuchte Polynom gefunden haben. Nun lässt sich auch die Qualität unserer bisherigen Abschätzungen der Wertetabellen der ersten und der zweiten Ableitung überprüfen (Polygonzüge für die geschätzten Wertetabellen, durchgezogene Linie für die exakten Graphen, schwarz=erste Ableitung, rot=zweite Ableitung):
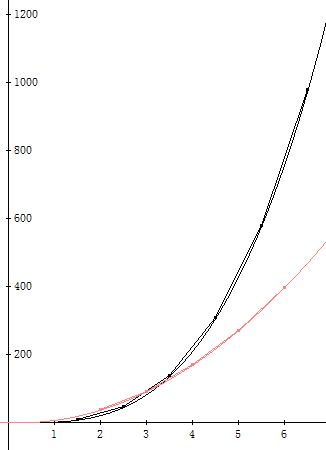
Die Abweichungen sind – vor allem bei der zweiten Ableitung – kaum sichtbar. Rechnerisch sind aber Abweichungen feststellbar, indem man Fragen dieser Art nachgeht: „An welcher Stelle ist die Steigung von f gleich 8?“ Ansatz: 4x3-3x2=8; reelle Lösung näherungsweise: x = 1.565775822. Der geschätzte Wert weicht davon um weniger als 7% ab. Bei weiteren geschätzten Werten ist die Abweichung noch geringer. Betrachtet man einen Bereich in der Nähe von (0|0) mit einer gezoomten Skalierung, so erkennt man:

Fazit: Die explizite Darstellung des allgemeinen Gliedes einer Folge, deren Anfangsglieder bekannt sind, gelingt erfolgreich insbesondere dann, wenn die Differenzenfolgen von Differenzenfolgen auf eine konstante Differenzenfolge stoßen. Ist die k-te Differenzenfolge konstant, so hat das durch eine Wertefolge gegebene Polynom den kleinsten Grad k.