Ist die folgende Abbildung linear? Bestimme ggf. die Matrix

Question

Aufgabe:

Ist die folgende Abbildung linear? Bestimme gegebenenfalls die zugehörige Matrix.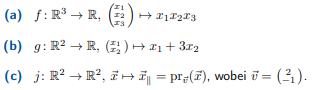

Text erkannt:

(a) \( f: \mathbb{R}^{3} \rightarrow \mathbb{R},\left(\begin{array}{l}x_{1} \\ x_{2} \\ x_{3}\end{array}\right) \mapsto x_{1} x_{2} x_{3} \)
(b) \( g: \mathbb{R}^{2} \rightarrow \mathbb{R},\left(\begin{array}{l}x_{1} \\ x_{2}\end{array}\right) \mapsto x_{1}+3 x_{2} \)
(c) \( j: \mathbb{R}^{2} \rightarrow \mathbb{R}^{2}, \vec{x} \mapsto \vec{x}_{\|}=\operatorname{pr}_{\vec{v}}(\vec{x}), \) wobei \( \vec{v}=\left(\frac{2}{-1}\right) \)

Problem/Ansatz: Also, was ich weiß ist, dass die Bedingung das etwas linear ist folgende ist:

f(x+y) = f(x) + f(y)

f(λ*x) = λ*f(x)

für alle λ∈ℝ

und x,y ∈ℝ

Ich verstehe aber nicht genau wie ich das anwenden soll und bei Aufgabe c verstehe ich nicht was pr_v bedeuten soll.

!

Answer 1

Aloha :)

zu a) nicht linear, denn:$$f(a\vec x)=a\begin{pmatrix}x_1\\x_2\\x_3\end{pmatrix}=\begin{pmatrix}ax_1\\ax_2\\ax_3\end{pmatrix}=ax_1ax_2ax_3=a^3x_1x_2x_3=a^3f(\vec x)\ne af(\vec x)$$zu b) linear, denn wir können eine Matrix angeben:$$g(\vec x)=x_1+3x_2=\begin{pmatrix}1 & 3\end{pmatrix}\binom{x_1}{x_2}$$zu c) linear, denn wir können eine Matrix angeben:$$\vec{\jmath}(\vec x)=\frac{1}{\sqrt5}\binom{2}{-1}\binom{x_1}{x_2}=\frac{1}{\sqrt5}(2x_1-x_2)=\frac{2}{\sqrt5}x_1-\frac{1}{\sqrt5}x_2=\begin{pmatrix}\frac{2}{\sqrt5} & -\frac{1}{\sqrt5}\end{pmatrix}\binom{x_1}{x_2}$$

Answer 2

a) ist nicht linear

                     1                           2
Berechne   f(  1   )       und   f ( 2    )
                      1                          2

b) ist linear. Die Matrix ist

(1    3)