Aufgabe: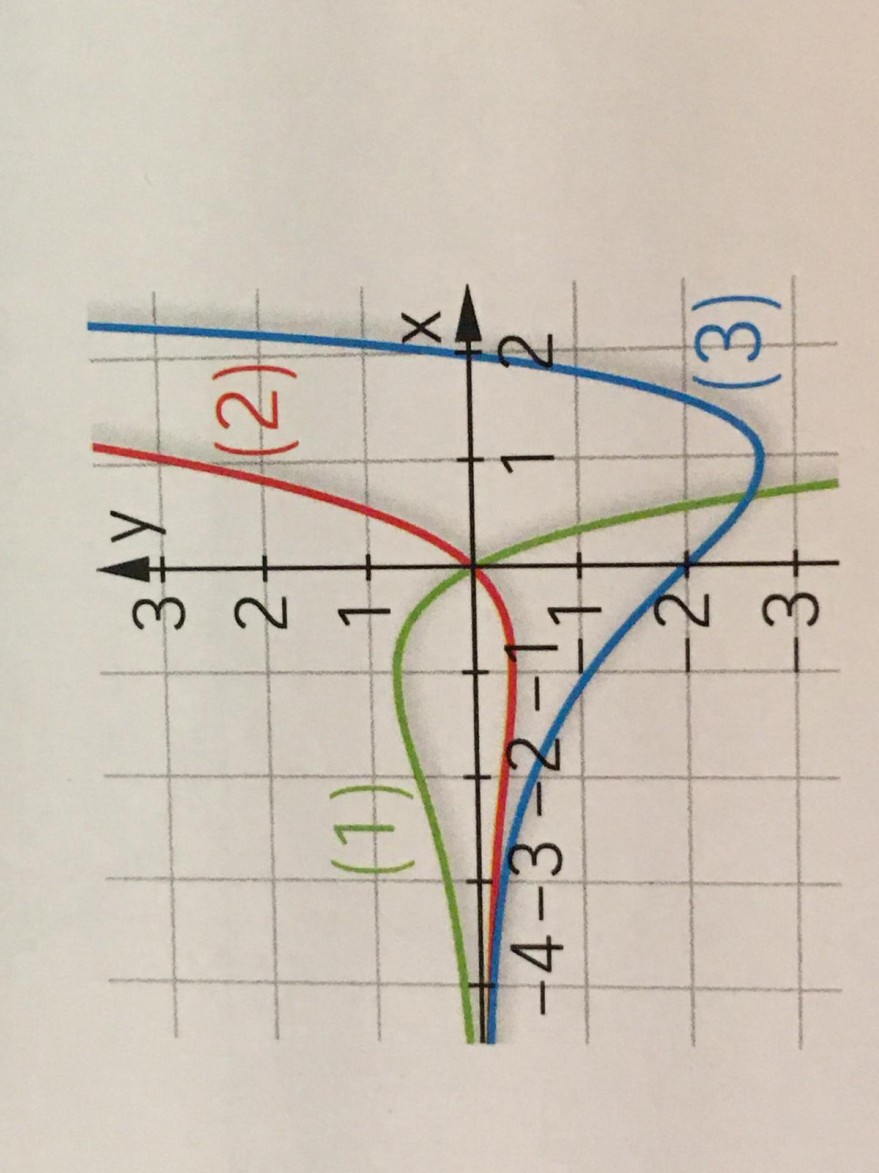
Was passiert, wenn man eine lineare Funktion l(x)=ax+b mit einer Exponentialfunktion g(x)=e^kx zu f(x)=(ax+b)*e^kx verknüpft?
a) Ordne begründet den Funktionsgleichungen f(x)= (x-2)*e^x , g(x)= -2x*e^x , h(x)= x*e^x passende Grafiken zu (siehe Abb.)
b) Untersuche die Funkionen jeweils auf Nullstellen, Extrempunkte und Wendepunkte. Gebe Begründungen für das Verhalten der Funktionen x -> ±∞
c) Forschungsaufgabe mit CAS: Zeige, dass alle Funktionen f(x)=(ax+b) *e^cx für a≠0 und c≠0 genau eine Nullstelle einen Extrempunkt und einen Wendepunkt besitzen.
Problem/Ansatz:
Hallo, ich muss diese Aufgaben in Mathe abgeben, leider ist Mathe gar nicht meins, ich belege es als Abdecker, da es Pflicht ist. Somit habe ich so gut wie keine Ahnung, wie ich hier vorgehen muss. Bis jetzt habe ich folgenden Ansatz; die Funktionen von a) kann ich den Graphen zuordnen, dazu habe ich einfach die Funktionen vom TS jeweils als Graphen zeichnen lassen. Begründen kann ich hierzu jedoch leider nichts. zu b) und c) habe ich gar keine Ansätze. Ich bin für jede Antwort hier dankbar, schonmal vielen Dank im Voraus!
Liebe Grüße :)