Skizziere komplexe Punktmengen. Bsp. {z Element C | Re(z) + 3Im(z) ≥ 3, |z-i | <1}

Question

ich habe noch ziemliche Probleme beim Umgang mit den komplexen Zahlen.

Ich soll folgende Mengen skizzieren:

{z Element C | Re(z) + 3Im(z) ≥ 3, |z-i | <1}

\( \{z \in C: 0<\operatorname{Re}(z) \leq 2,-1 \leq \operatorname{Im}(z)<2\} \)

\( \left\{z \in C: z=1, \operatorname{Re}\left(z^{2}\right) \geq 0\right\} \)

Vorallem verwirrt mich noch die Identifizierung einer komplexen mit einer reellen Zahl. Ist dies nur möglich, wenn der Imaginäranteil 0 ist?

Der Drucker hat die Betragstriche nicht abgedruckt.

Ich habe mal eine Skizze gemacht, wie ich die Mengen skizzieren würdeDer Drucker hat die Betragstriche nicht abgedruckt.:

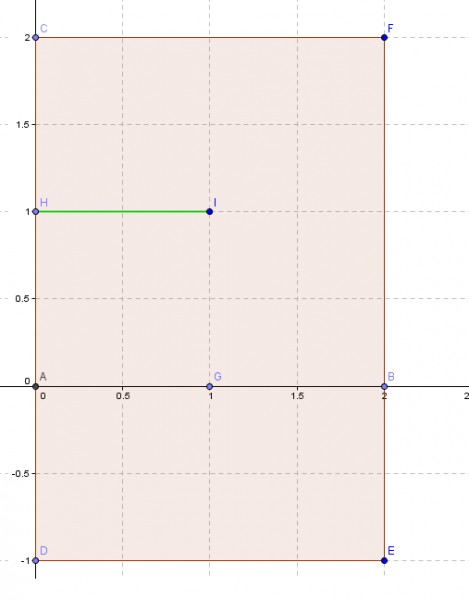
Die erste Menge sei die grüne Strecke (allerdings ohne Punkt (1|1), die zweite die eingefärbte Fläche und die dritte einfach der Punkt G mit (1|0). Das kommt mir selbst alles etwas sehr simpel vor.

Comments

1.

z-i < 1

ist etwas erstaunlich. Habt ihr für beliebige z eine Ordnung 'kleiner' definiert? Und wenn ja, wie denn?

i > -1 oder was?

2. Die 2. Menge hätte ich auch so skizziert. Einzig die beiden Ränder die nicht zur Menge gehören noch 'gestrichelt' zeichnen.

---

z-i < 1 steht zumindest auf meinem Blatt. Man vermisst den Betrag etwas, oder?  Ich hatte mir folgendes überlegt: z-1 = a+(b-1)*i

Da ich z doch auch hier auf eine reelle Zahl definiere (?) (eine < 1) soll z nur auf höhe von i liegen, damit somit der imaginäre Anteil entfällt.

Bei  der 2. hast du natürlich recht.

Answer 1

z= x+iy

z^2 = (x +iy)^2 = x^2 + 2ixy - y^2

Re(z^2) = x^2 - y^2 ≥ 0

x^2 ≥ y^2

|y|<|x|

Ich nehme nun einfach einmal an, dass man die Betragstriche nicht sieht.

z=1 wäre ja nur ein Punkt.

|z| = 1 heisst

x^2 + y^2 = 1. (Einheitskreis)

Daher 

2 Viertelkreisbogen ohne Rand.

Auch das erste Gebiet unter der Annahme, dass man den Betrag aus irgendeinem Grund nicht sieht.

|z-i| < 1 Inneres der Kreisscheibe mit Radius 1 um i.

und x + 3y ≥ 3

3y ≥ 3-x

y≥ 1 - 1/3x

Comments

Habe gerdae nochmal nachgeschaut, mein Drucker hat tatsächlich einfach die Betragsstriche nicht abgedruckt. Vielen Dank für die Aufklärung, ich hatte schon sehr gezweifelt!

---

Bitte! Gern geschehen! So was geschieht gelegentlich. Besser du zweifelst am Drucker als an der Mathematik.