Wie funktioniert die Nullstellenberechnung bei f(x)= 1/10 x^5 - x^2?

Question

wie berechnet man von

f(x)= 1/10 x^5 - x^2

alle Nullstellen?

Bitte, wenn es geht, die komplette Lösung angeben, bzw. den Rechenweg.

Vielen Dank

Answer 1

Erst einmal das Disrtibutivgesetz anwenden.

f(x)=1/10 x^5-x^2= x²(1/10 x³-1)

0=x²(1/10 x³-1)       bedeutet doppelte Nullstelle  x_1,2 =0  

0=1/10 x³-1    |+1

1=1/10 x³       |*10

10=x³                                                                  x_3,4,5=±(10^1/3)

 

 

Comments

Alles super. Nur: x_3,4,5=± 10^1/3 ohne ±, da negative Zahlen ^3 immer noch negativ sind.

Also: x_3,4,5= 10^1/3

Korrektur meiner Korrektur (Erklärung unten)

x₃ = 10^1/3 einfache Nullstelle. Keine weiteren Nullstellen.

---

Besser mit der KLammer ?

---

nein. 

- 10^{1/3} = - 2.1544

(- 10^{1/3})³ = (- 2.1544)³ = -10 ist nicht 10. Deshalb hier kein - in der Lösung möglich.

Es gilt wirklich nur: x₃= 10^1/3 = 2.1544

Du kannst zur Kontrolle auch den Graph zeichnen. Nur 2.1544 ist eine zusätzliche Nullstelle.

und die ist nicht mal dreifach.

 

 

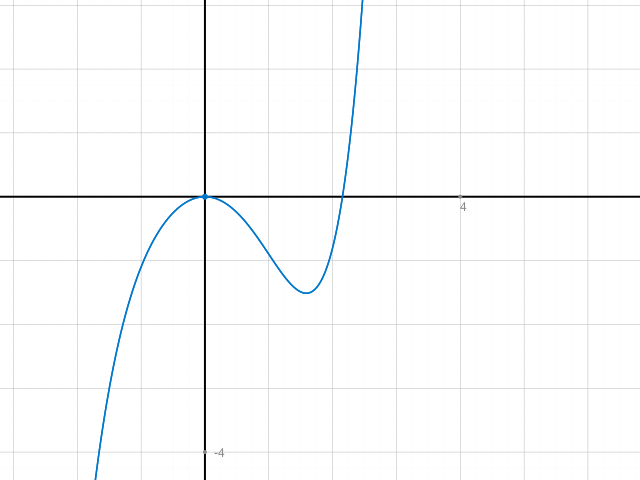
Betrachte auch noch g(x) = x^3 - 10 im Vergleich mit f(x)

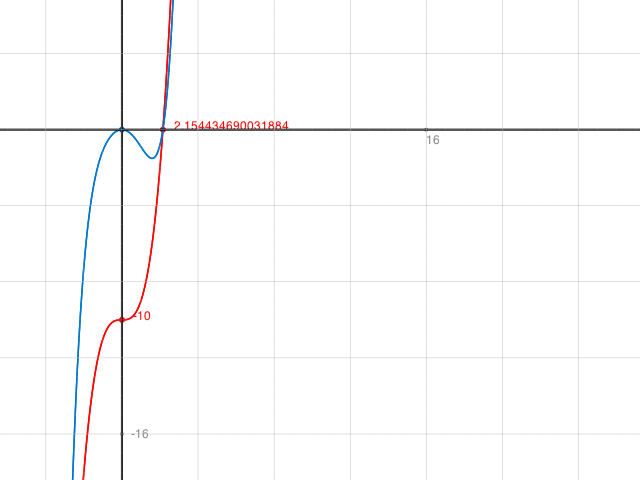
Der Terrassenpunkt von g befindet sich nicht bei der Nullstelle, sondern bei (0/-10).