ich habe eine Frage zu folgender Aufgabenstellung:
Text erkannt:
Berechnen Sie das Volumen...
a) \( \ldots \) des durch
$$ \vec{a}=\left(\begin{array}{c} 2 \\ -1 \\ 0 \end{array}\right), \quad \vec{b}=\left(\begin{array}{l} 0 \\ 2 \\ 3 \end{array}\right), \quad \vec{c}=\left(\begin{array}{c} 3 \\ 0 \\ -1 \end{array}\right) $$
aufgespannten Spats.
b) \( \ldots \) des durch
$$ \vec{a}=\left(\begin{array}{l} 1 \\ 2 \\ 3 \end{array}\right), \quad \vec{b}=\left(\begin{array}{l} 2 \\ 3 \\ 4 \end{array}\right), \quad \vec{c}=\left(\begin{array}{l} 2 \\ 2 \\ 2 \end{array}\right) $$
aufgespannten Tetraeders.
Ist meine Rechnung für a) soweit korrekt? Und ist -13 bzw. 13 nun der Flächeninhalt? Wenn nein, wie mache ich an der Stelle weiter? Ich habe die Sarrus-Regel angewendet und so die "echte Determinate" bestimmt.
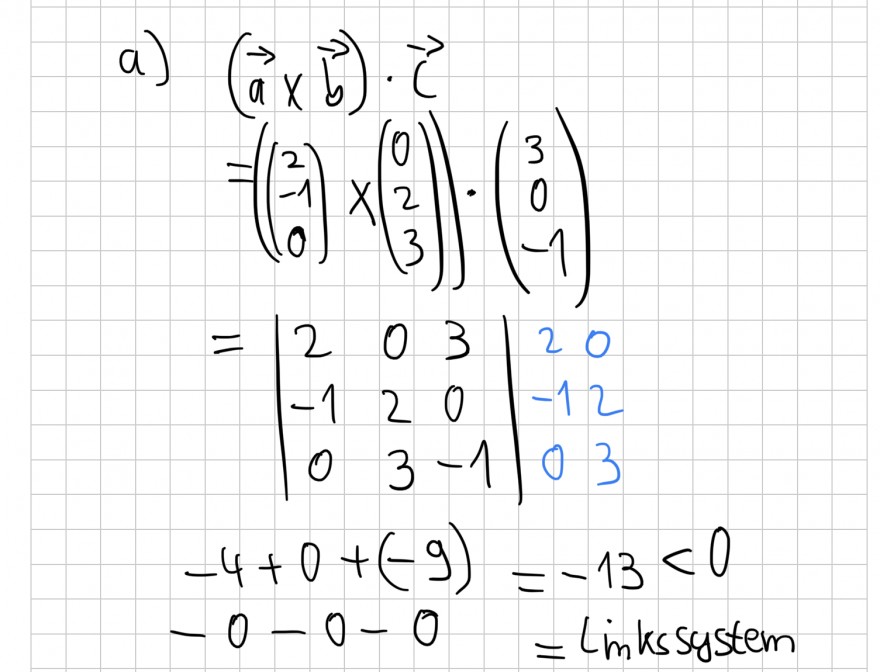
Wie sähe die Herangehensweise für b) aus?
Danke schon mal für eure Antworten!