Hallo Tessaa,
alle Aussagen oben, sind 'Wenn-dann' Aussagen. Es wird also einem Viereck (oder Dreieck bei a)) noch eine zusätzliche Eigenschaft mitgegeben und dann behauptet, dass es sich um einen weiteren Typ von Viereck handelt.
Zum Beispiel bei d)
Ein Parallelogramm plus gleich lange Diagonalen soll ein Rechteck sein. Da kann man z.B. fragen, was ein Rechteck von einem (allgemeinen) Parallogramm unterscheidet. Antwort: ein Rechteck hat zusätzlich einen Umkreis.
Wobei ich nun nicht weiß, ob Du diese Information benutzen darfst.
Beweis:
Bei jedem Parallelogramm halbieren sich die Diagonalen gegenseitig. Wenn die Diagonalen gleich lang sind, sind auch ihre Hälften gleich lang. Folglich geht in diesem Fall ein Kreis mit Mittelpunkt im Diagonalenschnittpunkt und mit dem Radius einer halben Diagonalenlänge durch alle vier Eckpunkte des Parallelogramms und ist somit der Umkreis des Parallelogramms. Folglich ist dieses Parallelogramm ein Rechteck.
Tipp: der Beweis zu b) ist zu diesem hier völlig identisch!
zu e) die Aussage ist falsch, es muss heißen "... dann handelt es sich um eine Raute" und ist somit identisch zu f)
zu f) Hier ist ein Parallelogramm gegeben und zusätzlich sollen die Diagonalen senkrecht aufeinander stehen, damit es eine Raute wird.
Was unterscheidet ein (allgemeines) Parallelogramm von einer Raute? Antwort: Eine Raute hat zusätzlich einen Inkreis; oder 2. und gleichwertige Antwort: zwei benachbarte Seiten sind gleich lang. Dazu eine kleine Skizze:
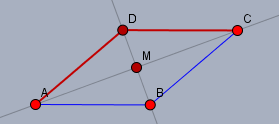
In einem Parallelogramm halbieren sich die Diagonalen. Also ist \(|AM| = |MC|\). Stehen die Diagonalen senkrecht zueinander, so ist \(\angle DMA = \angle CMD = 90°\), Folglich sind die beiden Dreiecke \(\triangle AMD\) und \(\triangle MCD\) kongruent, da sie in zwei Seiten \(|AM| = |MC|\) und \(|MD|\) und im erwähnten Winkel überein stimmen. Also müssen auch die Seiten \(AD\) und \(CD\) (rot) gleich lang sein. Folglich ist dieses Parallelogramm auch eine Raute.
Versuche Dich an den anderen Aufgaben mal selbst und überprüfe die Aufgabenstellung von c) und e), diese Aussagen sind falsch. Falls Du Fragen hast, so melde Dich bitte.