Extremwertprobleme Dreieck wie?

Question

Aufgabe:

Der Punkt P(u/f(u)) liegt auf den Graphen der Funktion f mit f(x)=-4x^2+4. Wie ist u zu wählen damit das Dreieck PQR mit Q (-2/0) und R(u/0) maximalen Flächeninhalt hat.

Problem/Ansatz:

bei der Zielfunktion scheitert es schon

Vielen Dank im Voraus

Answer 1

Hier die Skizze
R muß allerdings rechts der y-Achse liegen,

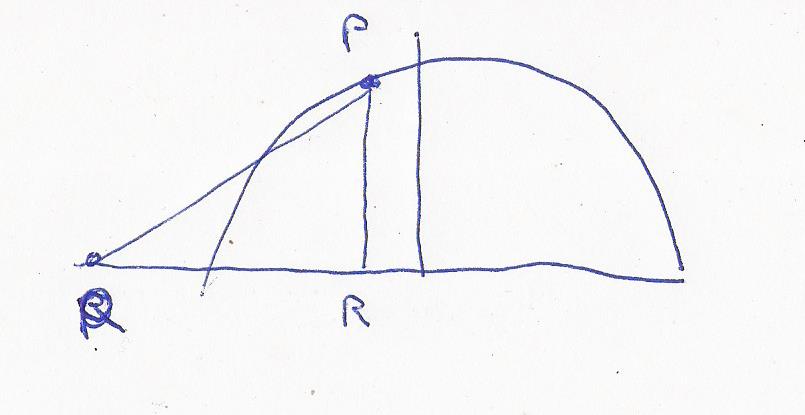
u ist positv.

Grundseite
| -2 | + u
Höhe Dreieck : f ( u ) = - 4 * u^2 + 4

Dreieck A = Grundseite * Höhe / 2
A ( u ) =  ( 2 + u ) * ( -4 * u^2 + 4 ) / 2
A ( u ) = - 2*u^3 - 4*u^2 + 2*u + 4
A ´( u ) = - 6*u^2 - 8*u + 2
Extremwert
- 6*u^2 - 8*u + 2 = 0

Bei Bedarf nachfragen