Die globalen min/max Werte sind die
größten/kleinsten Werte die eine Funktion
annehmen kann.
Die lokalen Extremwerte sind meistens Stellen
bei denen die Steigung null ist.
f ´( x ) = -2 * x * e^(-2*x)*(x - 1)
Stellen mit waagerechter Tangente
-2 * x * e^(-2*x)*(x - 1) = 0
Satz vom Nullprodukt anwenden
x = 0
e^(-2*x) | geht nicht
x - 1 = 0
x = 1
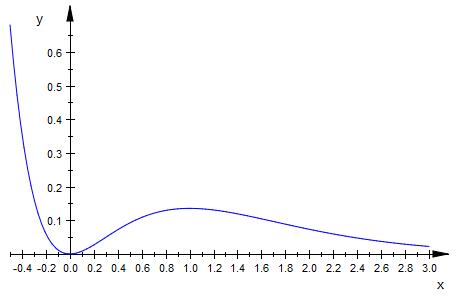
Bei x = 0 und x = 1 ist eine Stelle mit
waagerechter Tangente
2.Ableitung
f ´´ ( x ) = 2 * e^(-2*x) * (2*x^2 - 4*x + 1)
Wendepunkte
Satz vom Nullprodukt
2 * e^(-2*x) * (2*x^2 - 4*x + 1)
2*x^2 - 4*x + 1 = 0
x = 0.293
und
x = 1.707
Ich habe nicht alle Rechenschritte ausführlich
angeführt, kann das aber noch vorführen.
Frag nach.