Funktionale Abhängigkeiten im Koordinatensystem
Von den Vierecken \(A B_nCD\) liegen die Punkte C \((x_C|4)\) und \(B_n (x|y)\) auf der Geraden g mit der Gleichung \(y=\frac{4}{3} x-1,5\) .
Es gilt: A \((-1,5|-1)\); D \((-1,5|4)\).
a) Zeichne das Viereck AB1CD für \(x= \red {1,5}\) in ein Koordinatensystem ein:
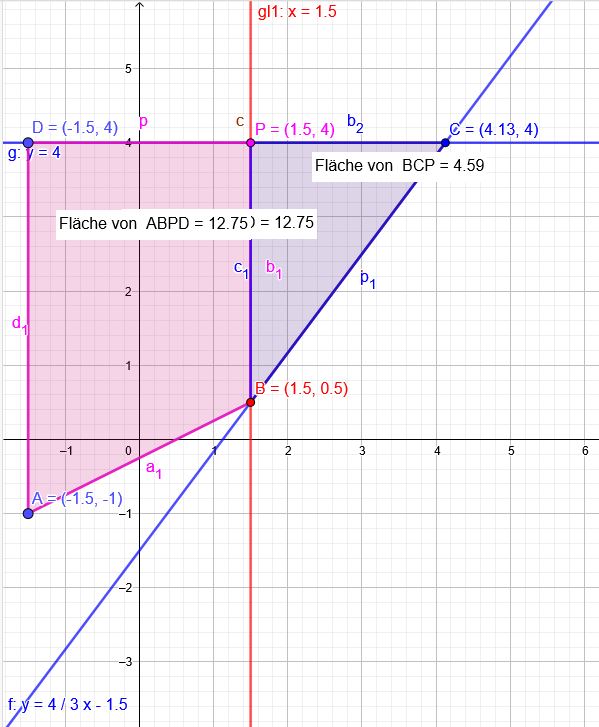
b) Berechne \(x_C\) und den Flächeninhalt A1 des Vierecks AB1CD.
Der Punkt C hat \(\red {4}\) als y-Koordinate.
C liegt auf der Geraden \(y=\frac{4}{3} x-1,5\)
\(\red {4}=\frac{4}{3} x-1,5\) Nach x auflösen:
\(4\cdot 3= 4 x-3 \cdot 1,5\)
\(16,5= 4 x\)
\(x_C=\orange{4,125}\)
Die Gerade durch B \(x= \red {1,5}\) schneidet die Gerade \(y=\blue{4}\) in P\((\red {1,5}|\blue{4})\)
Das Viereck ABPD ist ein Trapez:
\(A_T=0,5\cdot(\overline{AD}+\overline{BP})\cdot \overline{DP} \):
\(\overline{AD}=4+|-1|=5 \)
\(\overline{BP}=4-0,5=3,5 \)
\(\overline{DP}=|-1,5|+1,5=3 \)
\(A_T=0,5\cdot(5+3,5)\cdot 3=12,75 \)
Das Dreieck BCP ist rechtwinklig:
\(A_D=0,5 \cdot \overline{BP} \cdot \overline{PC} \):
\( \overline{BP} =4-0,5=3,5 \)
\( \overline{PC}=\orange{4,125}-1,5=2,625 \)
\(A_D=0,5 \cdot 3,5 \cdot 2,625=4,593 \)
c) Für welches x ergibt sich ein Trapez? Berechne den zugehörigen Flächeninhalt A2.
Aus obiger Zeichnung ergibt \(x= \orange{4,125}\) ein Trapez, weil dann parallel zu AD.
Geradengleichung durch A\(-1,5|-1) und B\(1,5|0,5)
\(y=0,5x-0,25\)
Schnitt mit \(x= \orange{4,125}\):
\(y=0,5\cdot 4,125 -0,25=1,8125\)
\(B_3(4,125|1,8125)\)
u.s.w.