Prädikatenlogik mit Quantoren: Welche Bedingung erfülle ich hier nicht?

Question

Ich habe folgende Aufgabe:

Das Universum für die Variable x ist N (Natürliche Zahlen inkl. 0) und für die Variable y und z ist das Universum Z (Ganze Zahlen). Geben Sie die Menge L von N an, für die das Prädikat erfüllt ist.

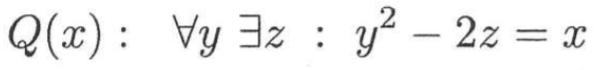
Text erkannt:

\( Q(x): \quad \forall y \exists z: y^{2}-2 z=x \)

Meine Vorgehensweise:

Ich habe mal das Prädikat aufgeschrieben: "Für alle y gibt es mindestens ein z, welche die Gleichung y² - 2x = x wahr macht"

D.h. ich suche ein z, sodass ich für alle y die Gleichung erfüllen kann.

Jetzt wäre meine Lösung L={0}

Da z.B. 0² - 2*0 = 0

Die Lösung meines Lehrer ist die leere Menge.

Warum stimmt meine Lösung nicht?

Vielen Dank im Voraus!

LG
Apple

Comments

D.h. ich suche ein z, sodass ich für alle y die Gleichung erfüllen kann.

Nein, du suchst alle festen x ∈ ℕ so , dass es zu jedem y ∈ ℤ ein passendes z ∈ ℤ gibt.

---

Wolfgang

Danke vielmals für Ihre Antwort. Leider, habe ich es nicht ganz verstanden.

Was meinen Sie mit "festen"?

Heisst das nun folgendes:

Ich bestimme zuerst das x. Ich suche ein z ∈ ℤ für jedes y ∈ ℤ, damit die Gleichung auf das bestimmte x aufgeht.

Die Menge L, welche ich herausfinden muss, beschreibt nun eigentlich das x. Ist das so?

Angenommen ich setzte für x = 0, dann ist es so, dass die Gleichung nicht für alle Y giltet (z.B. 1 - 2*z=0). Da es kein z gibt, welches ich einsetzen könnte.

Vielen Dank im Voraus!

LG
Apple

---

Was meinen Sie mit "festen" x?
Ich bestimme zuerst das x

L = { x∈ℕ |  ∀ y∈ℤ  ∃ z∈ℤ : y² - 2z = x }

Du musst doch für jede Überprüfung der Bedingung zuerst einmal x  festlegen.

---

Wolfgang

Danke jetzt habe ich es verstanden. Das ich zuerst das x festlegen muss.

Danke vielmals!

LG
Apple

---

Guten Tag Wolfgang und Apple

Ich habe eine Frage zu dieser Aufgabe. Heisst das, dass ich für x jede natürliche Zahl einsetzen muss und überprüfen muss, ob dies gehen würde?

LG
Pfizer

Answer 1

0 ist keine Lösung; denn die Aussage

∀ y∈ℤ  ∃ z∈ℤ : y^2 - 2z = 0

ist nicht wahr, weil z.B für y=3 es kein z gibt mit 9-2z=0.