Ich habe das mal ausprobiert und ich denke, dass das Verfahren für diese Matrix nicht konvergiert, siehe die ersten 10 Iterationen in der folgenden Grafik.
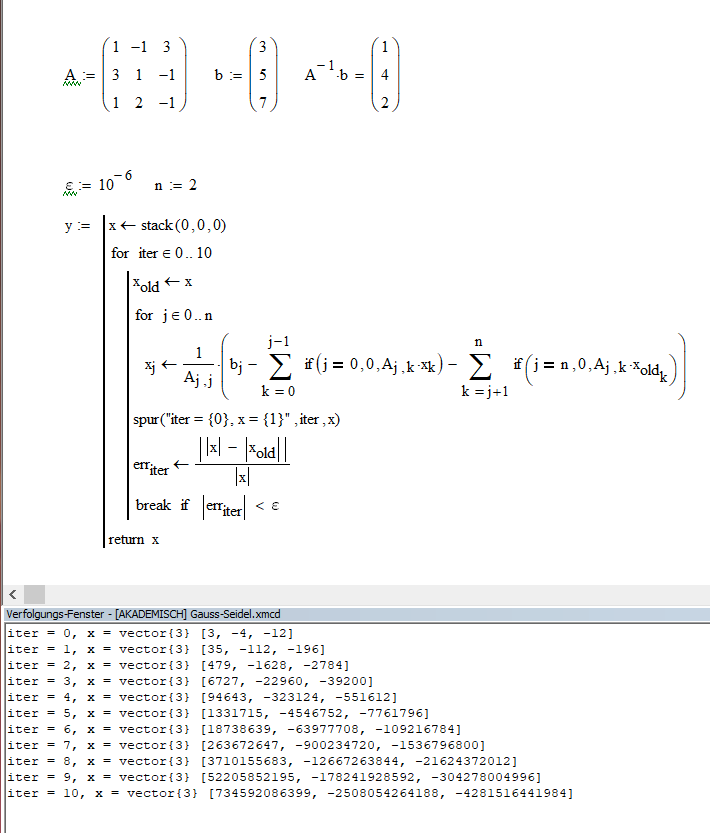
Bei einer anderen Matrix konvergiert das Verfahren, sihe folgende Grafik.
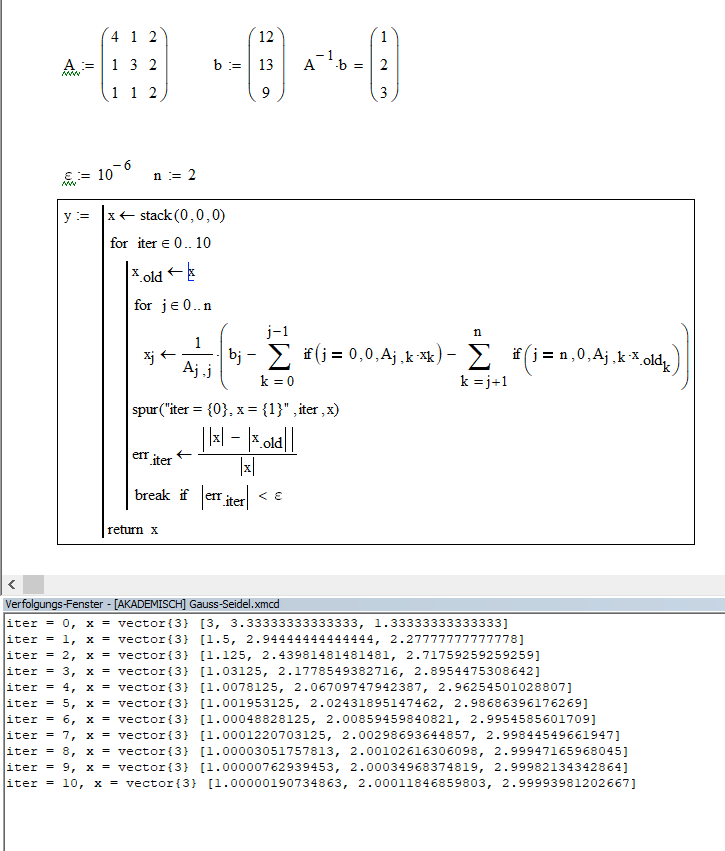
Der Grund liegt in dem Spektralradius der Matrix $$ I - B^{-1} A $$ mit \( B \) = untere Dreiecksmatrix der Matrix \( A \) (inkl. der Diagonalen). Der muss kleiner 1 sein, was in Deinem Beispiel nicht der Fall ist, aber imzweiten Beispiel.