1.)Tiefpunkt (260|0) Hier ist eine waagerechte Tangente → doppelte Nullstelle.
2.)waagerecht im Punkt B (0|130) → Hochpunkt
Nullstellenform der kubischen Parabel:
f(x)=a*(x-N_1)*(x-N_2)*(x-N_3)
f(x)=a*(x-260)^2*(x-N)
B (0|130)
f(0)=a*(0-260)^2*(0-N)
A.) 260^2*a*(-N_3)=130|:130
260^2*a*(-N)=130|:130
-520*a*N=1→a = - \( \frac{1}{520N} \)
f(x)= - \( \frac{1}{520N} \)•[(x-260)^2*(x-N)]
waagerechte Tangente im Hochpunkt B (0|130)
f´(x)=- \( \frac{1}{520N} \)•[2*(x-260)*(x-N)+(x-260)^2]
f´(0)=- \( \frac{1}{520N} \)•[2*(0-260)*(0-N)+(0-260)^2]
- \( \frac{1}{520N} \)•[2*(0-260)*(0-N)+(0-260)^2]=130
Mit Wolfram :
N=-270400/2081≈-129,9
a ≈ 2081/140608000
a ≈ \( \frac{2081}{140608000} \)
f(x)=\( \frac{2081}{140608000} \) •(x-260)^2*(x+270400/2081)
mfG
Moliets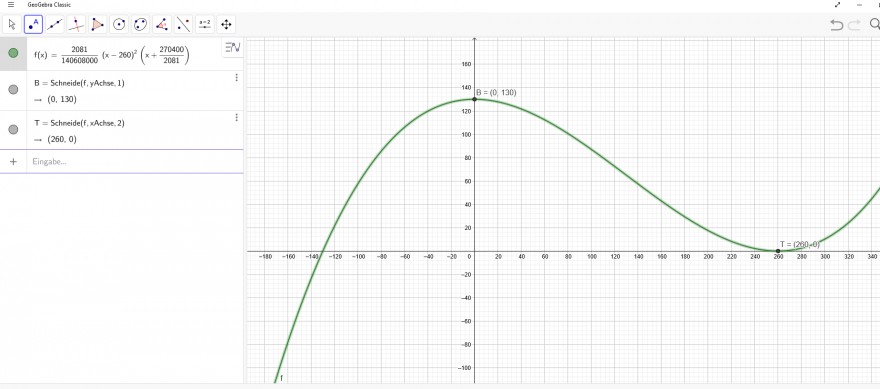
Text erkannt:
\( f(x)=\frac{2060000}{140060600}(x-260)^{2}\left(x+\frac{270000}{2001}\right) \)
\( -(0,130) \)
ets