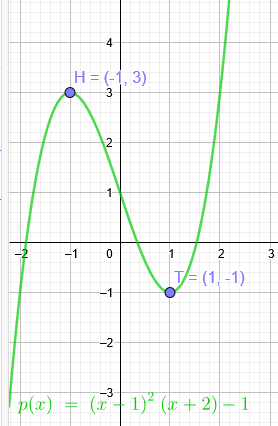
Eine Polynomfunktion 3. Grades hat den Tiefpunkt T(1| − 1) und den Hochpunkt H(−1|3).

Question

Aufgabe:

Eine Polynomfunktion 3. Grades hat den Tiefpunkt T(1| − 1) und den Hochpunkt
H(−1|3). Geben Sie den Term der Polynomfunktion an!

Answer 1

"Eine Polynomfunktion 3. Grades hat den Tiefpunkt T(1| − 1) und den Hochpunkt H(−1|3). Geben Sie den Term der Polynomfunktion an!"

f(x)=a*x^3+b*x^2+c*x+d

T(1| − 1)    f(1)=a+b+c+d

1.) a+b+c+d=-1

H(−1|3)   f(-1)=-a+b-c+d

2.)-a+b-c+d=3

f´(x)=3a*x^2+2b*x+c   f´(1)=3a+2b+c

3.)3a+2b+c=0

f´(-1)=3a-2b+c

4.)3a-2b+c=0

Löse nun das System.

Comments

"Eine Polynomfunktion 3. Grades hat den Tiefpunkt T(1| − 1) und den Hochpunkt H(−1|3). Geben Sie den Term der Polynomfunktion an!"

Weg über die Nullstellenform der kubischen Parabel:

T(1| − 1)→T(1| 0) doppelte Nullstelle:

\(f(x)=a*(x-1)^2*(x-N)\)

H(−1|3)→H´(−1|4)

\(f(-1)=a*(-1-1)^2*(-1-N)=4a*(-1-N)\)

\(4a*(-1-N)=4→a*(-1-N)=1→a=\frac{1}{-1-N}\)

\(f(x)=\frac{1}{-1-N}*[(x-1)^2*(x-N)]\)

\(f´(x)=0\)

\(f´(x)=\frac{1}{-1-N}*[(2x-2)*(x-N)+(x-1)^2*1]\)

\(f´(-1)=\frac{1}{-1-N}*[(2*(-1)-2)*(-1-N)+(-1-1)^2]\)

\(f´(-1)=\frac{1}{-1-N}*[(-4)*(-1-N)+4]\)

\(\frac{1}{-1-N}*[(-4)*(-1-N)+4]=0\)→\(N=-2\)→\(a=\frac{1}{-1+2}=1\)

\(f(x)=(x-1)^2*(x+2)\)

\(p(x)=(x-1)^2*(x+2)-1\)

Answer 2

Hallo,

\( f(x)=a x^{3}+b x^{2}+c x+d \)
\( f^{\prime}(x)=3 a x^{2}+2 b x+c \)

T und H liefern folgende Informationen:

\( T( 1 \mid1) \Rightarrow a+b+c+d=-1 \)
\( f^{\prime}(1)=0 \Rightarrow 3 a+2 b+c=0 \)
\( H(-1 \mid 3) \Rightarrow-a+b-c+d=3 \)
\( f^{\prime}(-1)=0 \Rightarrow 3 a-2 b+c=0 \)

Gruß, Silvia

Comments

Hallo Silvia, der Tiefpunkt soll bei T(1|-1) liegen.

---

Danke, Moliets, ich korrigiere das.