Das Schaubild einer Polynomfunktion 4.Grades geht durch den punkt s(0/2)
f(0) = 2
und hat den Wendepunkt W(1/ 31/12).
f(1) = 31/12
f''(1) = 0
Die Normale im Punkt P (-3/ 5/4) hat die Steigung 1/5.
f(-3) = 5/4
f'(-3) = -1/(1/5) = -5
Bestimmen Sie den Funktionsterm?
Die Gleichungen die entstehen
e = 2
a + b + c + d + e = 31/12
12·a + 6·b + 2·c = 0
81·a - 27·b + 9·c - 3·d + e = 5/4
-108·a + 27·b - 6·c + d = -5
Daraus ergibt sich dann die Funktion
f(x) = 1/12·x^4 - 1/2·x^2 + x + 2
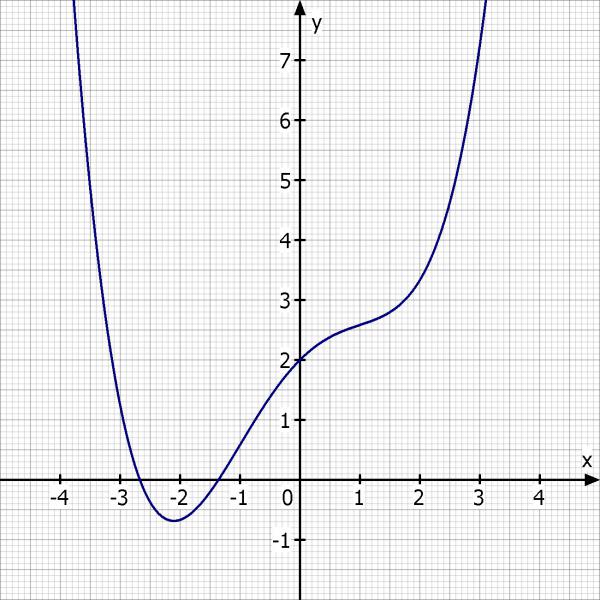
Skizze