Aloha :)
Um nicht alles in Latex tippen zu müssen, habe ich die Tabellen aus meinem Excel kopiert.
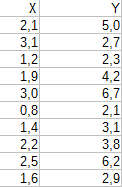
Wir sollen eine lineare Modellgleichung der Form$$y(x)=a\cdot x+b$$im Sinne der Methode der kleinsten Fehlerquadrate bestmöglich anpassen. Dazu setzen wir die \(x\)- und \(y\)-Werte aus der Tabelle ein und erhalten 10 Gleichungen für die beiden Unbekannte \(a\) und \(b\):
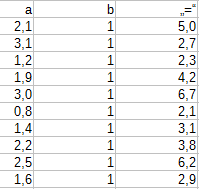
Dieses Gleichungssystem ist nicht eindeutig lösbar. Die Methodes der kleinsten Quadrate verlangt nun, dass wir beide Seiten des Gleichungssystem mit der transponierten Koeffizienten-Matrix multiplizieren:


Wir erhalten also als Gleichungssystem:$$\begin{pmatrix}44,32 & 19,80\\19,80 & 10,00\end{pmatrix}\binom{a}{b}=\binom{84,23}{39,00}$$und dieses hat die Lösung$$\binom{a}{b}=\binom{1,370211}{1,186982}$$Die gesuchte Ausgleichsgrade ist also:$$y=1,370211\cdot x+1,186982$$
~plot~ 1,370211*x+1,186982 ; {2,1|5,0} ; {3,1|2,7} ; {1,2|2,3} ; {1,9|4,2} ; {3,0|6,7} ; {0,8|2,1} ; {1,4|3,1} ; {2,2|3,8} ; {2,5|6,2} ; {1,6|2,9} ; [[0|3,5|0|7]] ~plot~