Hallo,
Drücken Sie die Gleichung x + y + z = 1 in Kugelkoordinaten aus.
schreibe ab, was hier steht, $$x = r \cdot \sin(\theta) \cdot \cos(\phi) \\ y = r \cdot \sin(\theta) \cdot \sin(\phi) \\ z = r \cdot \cos(\theta) $$und setze die Größen für \(x\), \(y\) und \(z\) in die gegebene Gleichung ein:$$\begin{aligned} r \cdot \sin(\theta) \cdot \cos(\phi) + r \cdot \sin(\theta) \cdot \sin(\phi) + r \cdot \cos(\theta) &= 1 \\ r(\sin(\theta) \cdot \cos(\phi) + \sin(\theta) \cdot \sin(\phi) + \cos(\theta)) &= 1 \\ r = \frac1{\sin(\theta) \cdot \cos(\phi) + \sin(\theta) \cdot \sin(\phi) + \cos(\theta)}\end{aligned}$$Bem.: achte darauf, wie der Winkel \(\theta\) in Deinem Umfeld definiert ist. Es sind auch andere Konventionen gebräuchlich!
Drücken Sie die Gleichung r = 2 sin(Φ) in kartesischen Koordinaten aus
Es gilt:$$\begin{aligned} x &= r \cdot \cos(\phi) \\ y &= r \cdot \sin(\phi) \quad \implies \sin(\phi) = \frac yr \\ r & = \sqrt{x^2 + y^2}\end{aligned}$$Das setze wieder in obige Gleichung ein:$$\begin{aligned} r &= 2 \sin(\phi) \\ \sqrt{x^2 + y^2} &= 2 \frac yr = 2 \frac{y}{\sqrt{x^2 + y^2}} && |\, \cdot \sqrt{x^2 + y^2} \\ x^2 + y^2 &= 2y && |\, -2y + 1 \\ x^2 + y^2 - 2y + 1 & = 1 \\ x^2 + (y-1)^2 &= 1 \end{aligned}$$und dies ist ein Kreis mit Radius \(1\) und Mittelpunkt \(M(0|\, 1)\) wie folgendes Bild zeigt:
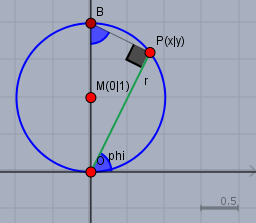
Die Strecke \(|OB|\) ist \(|OB|=2\). Den Winkel \(\phi\) (blau) in \(O\) findet man im rechtwinkligen Dreieck \(\triangle OPB\) wieder \(\angle OBP = \phi\). Folglich ist die grüne Strecke \(|OP| = r = |OB| \cdot \sin(\phi) = 2 \sin(\phi)\).
Falls Du dazu noch Fragen hast, so melde Dich bitte. Feedback jeder Art ist definiv erwünscht!
Gruß Werner