Liebe Lounge,
ich habe eine Frage zu Ober- und Untersummen einer auf I negativen Funktion f.
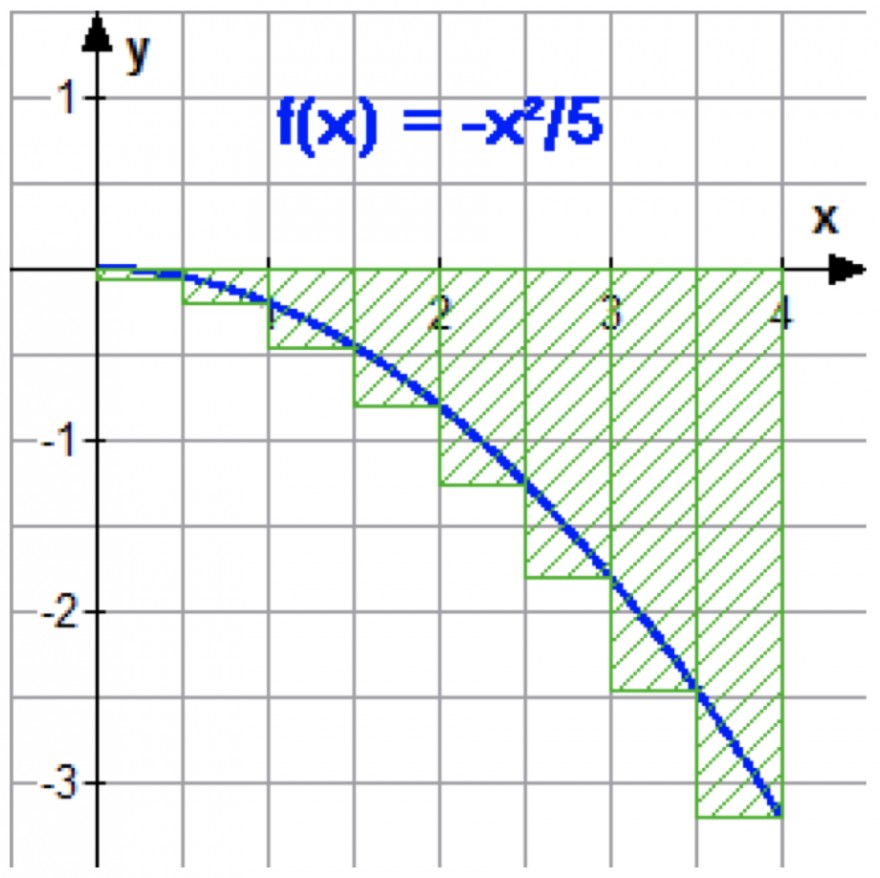
Das Integral (vgl. Abbildung) auf dem Intervall [0;4] ist ja in jedem Fall negativ. Deshalb sind sowohl OBer- als auch Untersumme negativ (abgebildet ist hier die Untersumme).
Ferner gilt: Untersumme ≤ Integral ≤ Obersumme.
Nun zu meiner Frage: Seien A und A1 orientierte Flächeninhalte. Dann gilt doch immer: Wenn A > A1 ist A die größere orientierte Fläche? Als Beispiel wäre demnach eine orientierte Fläche A=-1 größer! als A1=-2 , obwohl der Graph mit dem orientierten Flächeninhalt A1 ja augenscheinlich mehr Fläche einschließt ?