Zeigen Sie, dass f(D) offen ist.

Question

Hallo,

ich bräuchte bei der folgenden Aufgabe bitte eure Hilfe.

Sei D ⊂ Rⁿ offen und f : D → R stetig differenzierbar mit ∇f(x) ≠ 0 für alle x ∈ D.
Zeigen Sie, dass f(D) offen ist.

Answer 1

Hallo,

das ist eine direkte Folgerung aus dem Satz über die lokale Umkehrbarkeit. Ich habe mich mal um ein Bild in PowerPoint bemüht: Natürlich ohne die blauen Lücken dazwischen. :D

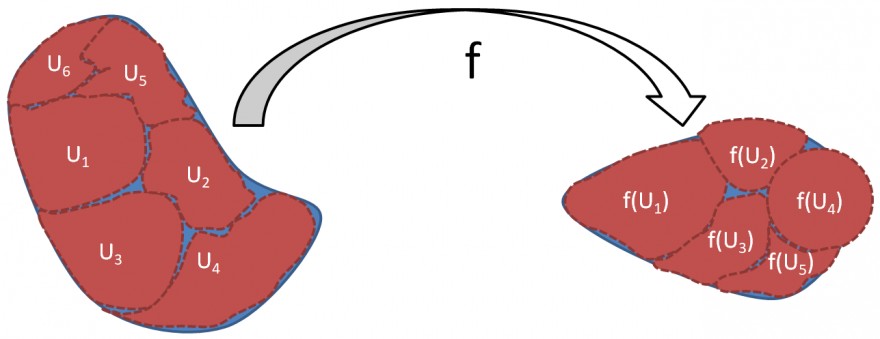
Jeder Punkt $x\in D$ besitzt nämlich nach dem Umkehrsatz eine offene Umgebung $U_x$, deren Bild $f(U_x)$ offen ist. Dann ist $f(D)=\bigcup\limits_{x\in D}f(U_x)$ offen und zusammenhängend. (Stetigkeit von $f$)