Aufgabe:
Text erkannt:
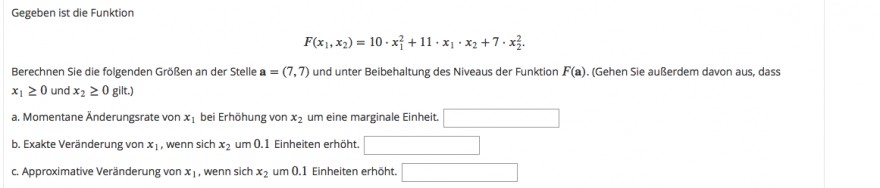
Gegeben ist die Funktion
$$ F\left(x_{1}, x_{2}\right)=10 \cdot x_{1}^{2}+11 \cdot x_{1} \cdot x_{2}+7 \cdot x_{2}^{2} $$
Berechnen Sie die folgenden Größen an der Stelle \( \mathbf{a}=(7,7) \) und unter Beibehaltung des Niveaus der Funktion \( F(\mathbf{a}) . \) (Gehen Sie außerdem davon aus, dass \( x_{1} \geq 0 \) und \( x_{2} \geq 0 \) gilt.)
a. Momentane Änderungsrate von \( x_{1} \) bei Erhōhung von \( x_{2} \) um eine marginale Einheit.
b. Exakte Veränderung von \( x_{1}, \) wenn sich \( x_{2} \) um 0.1 Einheiten erhöht.
c. Approximative Veränderung von \( x_{1} \), wenn sich \( x_{2} \) um 0.1 Einheiten erhōht.
Problem/Ansatz:
Leider finde ich auf Mathelounge keine ähnliche Aufgabe. Kann mir das jemand erklären?