bestimme eine Funktionsgleichung g(t) = a x bt + 18

Question

Aufgabe:

Leitidee des funktionalen Zusammenhangs

Zu Beginn wird der Wert 100 Grad gemessen, nach 2 Min hat der Pudding eine Temperatur von 84,42 Grad.

b) bestimme eine Funktionsgleichung g(t) = a x b^t + 18

Problem/Ansatz:

Wie kommt man bitte da auf g(t) = 82 x 0,9^t +18

Answer 1

"Zu Beginn wird der Wert 100 Grad gemessen, nach 2 Min hat der Pudding eine Temperatur von 84,42 Grad.

b) bestimme eine Funktionsgleichung g(t) = a * b^t + 18"

A(0|100)

g(0) = a * b^0 + 18   → $b^{0}$   =  1

a * 1 + 18=100

a=82


B(2|84,42)

g(2) = a * b^2 + 18

a * b^2 + 18=84,42

82 * b^2 + 18=84,42

b_1=0,9

[b_1=-0,9-> kommt nicht in Betracht]

g(t) =82* 0,9^t + 18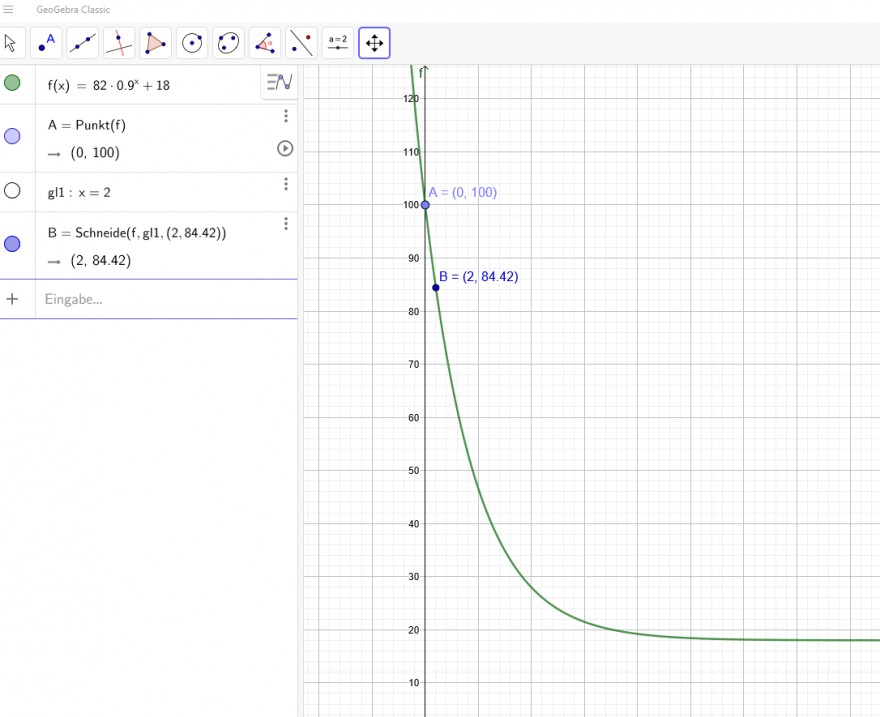

Text erkannt:

GeoGebra Classic
$f(x)=82 \cdot 0.9^{x}+18$
$\mathrm{A}=\operatorname{Punkt}(\mathrm{f})$
\begin{tabular}{l}
If \\
\hline
\end{tabular}
$\rightarrow(0,100)$

mfG

Moliets