Das Ergebnis was ich raus beklommen würde wäre ja dann (1 0
0 -1) oder?
Nein - gefragt ist doch nach der Spiegelmatrix \(S\). Wohin gegen$$X =\begin{pmatrix}1& 0\\ 0& -1\end{pmatrix}$$die Spiegelung an der X-Achse ist. Nicht mehr und nicht weniger.
Und \(S\) ist$$S =\begin{pmatrix}-0,6& 0,8\\ 0,8& 0,6\end{pmatrix}$$das ist das Ergebnis! Und bei der Herleitung des Ergebnisses für \(S\) ist es es egal ob Du den Ansatz über \(R \cdot X\) - wie in meiner Antwort oben - oder \(R \cdot Y\) benutzt - wie in meinem Kommentar von heute gezeigt.
Du kannst das doch leicht überprüfen: $$\begin{pmatrix}1& 0\\ 0& -1\end{pmatrix} \cdot \begin{pmatrix}3\\ 1\end{pmatrix} = \begin{pmatrix}3\\ -1\end{pmatrix} \ne q$$ Und $$\begin{pmatrix}-0,6& 0,8\\ 0,8& 0,6\end{pmatrix}\cdot \begin{pmatrix}3\\ 1\end{pmatrix} = \begin{pmatrix}-1,8 + 0,8\\ 2,4 + 0,6\end{pmatrix} = \begin{pmatrix}-1\\ 3\end{pmatrix} = q \space \checkmark$$Manchmal hilt auch eine Zeichnung:
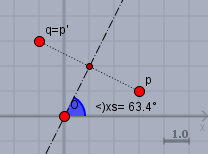
\(\cos(2 \cdot 63,43°)=-0,6\) und \(\sin(2 \cdot 63,43°) = 0,8\)