Bestimmen Sie die explizite Definition der Funktion f(t), die durch die Gleichung F(t, f(t))=2 implizit definiert …

Question

Aufgabe:

Text erkannt:

Es sei \( F(x, y)=20 x^{0.3} y^{0.6} \). Bestimmen Sie die explizite Definition der Funktion \( f(t), \) die durch die Gleichung \( F(t, f(t))=2 \) implizit definiert ist, und berechnen Sie \( f^{\prime}(t) \).

Problem/Ansatz: Ich benutze die Formel: y´(x)= -Fx/Fy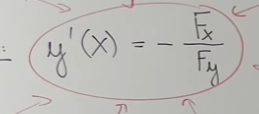

Text erkannt:

\( \left.y^{\prime}(x)=-\frac{F_{x}}{F_{y}}\right) \)

F(x,y) leite ich nach x ab und für y auch. Danach setzte ich alles in die Formel ein.

Aber es kommt immer das Falsche raus. Kann mir jemand Bitte helfen? Ich glaube diese Forml ist nur Gültig wenn die Gleichung y=0 ist.

Lösung: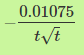

Text erkannt:

\( -\frac{0.01075}{t \sqrt{t}} \)

Answer 1

Aloha :)

$$\left.F(x;y)=20x^{0,3}y^{0,6}\stackrel!=2\quad\right|:\,20$$$$\left.x^{0,3}y^{0,6}=\frac{1}{10}\quad\right|\cdot x^{-0,3}$$$$\left.y^{0,6}=\frac{1}{10}x^{-0,3}\quad\right|\text{Exponenten in Brüche wandeln}$$$$\left.y^{\frac{3}{5}}=\frac{1}{10}x^{-\frac{3}{10}}\quad\right|(\cdots)^{\frac{5}{3}}$$$$\left.y=\frac{1}{10^{5/3}}x^{-\frac{3}{10}\cdot\frac{5}{3}}=\frac{1}{10^{5/3}}x^{-\frac{1}{2}}=\frac{10^{1/3}}{10^{6/3}}\frac{1}{\sqrt x}\quad\right.$$$$y=\frac{\sqrt[3]{10}}{100}\,\frac{1}{\sqrt x}$$Das sollen wir noch ableiten:$$y'(x)=\frac{\sqrt[3]{10}}{100}\,\cdot\left(-\frac{1}{2}\right)\frac{1}{x\sqrt x}=-\frac{\sqrt[3]{10}}{200}\,\frac{1}{x\sqrt x}\approx\frac{-0,010772}{x\sqrt x}$$

Answer 2

\( F(t, f(t))=2 \)

(\t\) und \(f(t)\) in \( F(x, y)=20 x^{0.3} y^{0.6} \) einsetzen ergibt

        \(F(t, f(t))=20 t^{0.3} f(t)^{0.6}\)

also

        \(20 t^{0.3} f(t)^{0.6} = 2\)

Auflösen nach \(f(t)\) ergibt

        \(f(t) = 0{,}1^{\frac{5}{3}} t^{-\frac{1}{2}}\)