Grenzwert gegen 0 mit Wurzel

Question

Aufgabe:

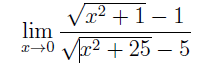
Text erkannt:

\( \lim \limits_{x \rightarrow 0} \frac{\sqrt{x^{2}+1}-1}{\sqrt{x^{2}+25}-5} \)

Problem/Ansatz:

Mithilfe der 3. Binom Formel bekomme ich oben den Zähler multipliziert mal den Nenner mit Ausnahme +5. Im neuen Zähler habe ich x^2. Danach komme ich nicht mehr weiter.

Comments

Hallo,

Du musst sowohl den Zähler als auch den Nenner jeweils passend mit Hilfe der 3. binomischen Formel erweitern, dann kürzt sich das \(x^2\) heraus und Du erhältst das Ergebnis von Werner-Salomon

Gruß

Answer 1

Hallo,

wende die Regel nach l'Hospital an:$$\lim_{x \to 0} \frac{\sqrt{x^{2}+1}-1}{\sqrt{x^{2}+25}-5}= \lim_{x \to 0}  \frac{\frac{x}{\sqrt{x^2+1}}}{\frac{x}{\sqrt{x^2+25}}} = \lim_{x \to 0}  \frac{\frac{1}{\sqrt{x^2+1}}}{\frac{1}{\sqrt{x^2+25}}} = \frac{\frac 11}{\frac 15} = 5$$