Hallo,
Aufgabe a)
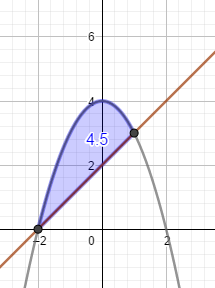
Um die Schnittpunkte zu ermitteln, setzt du die Funktionen gleich:
\(-x^2+4=x+2\\ -x^2-x+2=0\)
Mit \(h(x)=-x^2-x+2\) hast du gleichzeitig die Differenzfunktion gebildet, mit der du nachher das Integral berechnest.
Doch erst weiter mit den Schnittpunkten
\(-x^2-x+2=0\\x^2+x-2=0\\\text{pq-Formel ergibt}\\x_1=-2\quad \vee \quad x_2=1\)
Das sind die Grenzen des Integrals.
\(\int \limits_{a}^{b}f(x)dx=F(b)-F(a)\\ \int \limits_{-2}^{1}-x^2-x+2\quad dx=\bigg[-\frac{1}{3}x^3-\frac{1}{2}x^2+2x\bigg]_{-2}^1\\ =-\frac{1}{3}\cdot 1^3-\frac{1}{2}\cdot 1^2+2\cdot 1-(-\frac{1}{3}\cdot (-2)^3-\frac{1}{2}\cdot (-2)^2+2\cdot (-2))=4,5\)
Falls du noch Fragen zur Vorgehensweise hast, melde dich bitte.
Gruß, Silvia