Bestimmen Sie die Maßzahl der Fläche, die von den beiden Funktionsgraphen eingeschlossen wird.

Question

Hallo Leute! Ich brauche unbedingt eure Hilfe bei einer Aufgabe! Ich hoffe ihr könnt mir helfen! Ich bedanke mich schonmal im voraus!

Die Aufgabe:

a) Gegeben sind die Funktionen f und g durch
f(x)= −x² + 4; ∈R und g(x)= x + 2; ∈R
Bestimmen Sie die Maßzahl der Fläche, die von den beiden Funktionsgraphen eingeschlossen wird.

b) Gegeben sind die Funktionen f und g durch
f(x)= −x + 6; ∈R und g(x)= x² − 6∙x + 10; ∈R.
Bestimmen Sie die Maßzahl der eingeschlossenen Fläche zwischen den Graphen.

c) Gegeben sind die Funktionen f und g durch
f(x)= x³ − 9∙x; ∈R und g(x)= −5∙x; ∈R
Bestimmen Sie die Maßzahl der eingeschlossenen Fläche zwischen den Graphen.

SCHNITTPUNKTE: A(1/3), B(-2/0)

Answer 1

Hallo,

Aufgabe a)

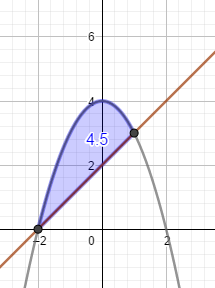
Um die Schnittpunkte zu ermitteln, setzt du die Funktionen gleich:

$-x^2+4=x+2\\ -x^2-x+2=0$

Mit $h(x)=-x^2-x+2$ hast du gleichzeitig die Differenzfunktion gebildet, mit der du nachher das Integral berechnest.

Doch erst weiter mit den Schnittpunkten

$-x^2-x+2=0\\x^2+x-2=0\\\text{pq-Formel ergibt}\\x_1=-2\quad \vee \quad x_2=1$

Das sind die Grenzen des Integrals.

$\int \limits_{a}^{b}f(x)dx=F(b)-F(a)\\ \int \limits_{-2}^{1}-x^2-x+2\quad dx=\bigg[-\frac{1}{3}x^3-\frac{1}{2}x^2+2x\bigg]_{-2}^1\\ =-\frac{1}{3}\cdot 1^3-\frac{1}{2}\cdot 1^2+2\cdot 1-(-\frac{1}{3}\cdot (-2)^3-\frac{1}{2}\cdot (-2)^2+2\cdot (-2))=4,5$

Falls du noch Fragen zur Vorgehensweise hast, melde dich bitte.

Gruß, Silvia

Comments

Vielen Dank!!! Das ist ja ziemlich einfach, wenn man die Vorgehensweise kennt. Haben noch 2 Fragen.

Muss man die Schnittpunkte berechnen, wenn man sie auch ablesen kann?

Gehe ich bei den nächsten 2 Aufgaben genauso vor? Da steht ja was anderes

(Bestimmen Sie die Maßzahl der eingeschlossenen Fläche zwischen den Graphen.) Gibt es dafür eine andere Vorgehensweise oder rechnet man die Aufgaben genauso wie a)

LG

---

Wenn du die Schnittpunkte ablesen kannst, reicht das natürlich.

Die nächsten beiden Aufgaben rechnest du ebenso. "Fläche, die von den beiden Funktionsgraphen eingeschlossen wird" ist nur eine andere Formulierung für "eingeschlossene Fläche zwischen den Graphen"

---

Bei b) habe ich 22,5 raus. Ist das richitg?

---

Ich komme wieder auf 4,5

---

bei mir ist f(x) - g(x) = x² + 5x - 4

Stimmt damit vielleicht etwas nicht?

---

Das Vorzeichen bei x² ist minus

f(x) - g(x) = -x² + 5x - 4

---

Ja bei mir auch, hab es nur vergessen gehabt zu tippen. Ich habe aber die gleichen Schnittpunkte wie bei a) genommen. Muss ich sie bei b) ausrechnen?

---

Ja, es sei denn, du liest sie von meiner Zeichnung ab.

---

Also muss ich bei b) die Schnittpunkte rechnerisch bestimmen, weil sie nicht die gleichen wie bei a) sind?

---

Ok, vielen dank!!!!!

---

Kannst du mir kurz zeigen, wie du die Schnittpunkte ausgerechnet hast? Verstehe ich gerade überhaupt nicht. Ich weiß, dass ich sie einfach von dir nehmen könnte, will es aber auch mal ausrechen :)

---

Setze die Differenzfunktion gleich 0:

$-x^2+5x-4=0\\x^2-5x+4=0\\ \text{pq-Formel}\\ x_{1,2}=2,5\pm\sqrt{2,5^2-4}\\ x_{1,2}=2,5\pm 1,5\\x_1=2\quad\text{und}\quad x_2=4$

---

Das ist mir jetzt peinlich! Ich hatte die ganze Zeit 2 und 4 raus. War aber voll verwirrt, weil bei den Graphen den du mir geschickt hast 1,5 und 4,2 waren. Sorry, für die vielen Fragen!

---

Grins, tja, ich wollte dir das Ablesen erleichtern und geogebra hat auch die y-Koordinaten mit angegeben. Bei Aufgabe c komme ich übrigens auf 8 FE.

---

Noch eine Kurze Frage. Wenn ich die pq formel jetzt eingebe, komme ich die ganze Zeit auf 1 und 4

---

bei b oder bei c?

---

Bei b, wo du 2 hast habe ich 1

---

Da hast du recht und ich mich verschrieben.

---

Bei c) habe ich jetzt x³ - 4x = 0

Wie mache ich jetzt weiter? Das kann ich ja schwer in die pq F einsetzen

---

Du klammerst x aus:

$x^3-4x=0\\ x(x^2-4)=0\\x=0\quad \vee\quad x^2-4=0$

Wegen der Symmetrie zum Ursprung reicht es, wenn du einen der beiden Flächeninhalte berechnest und dann verdoppelst.

---

Tut mir leid, ich verstehe nicht ganz. Kann mich auch gar nicht erinnern, dass ich das mal in der Schule gemacht habe. Wie soll ich die Fläche denn jetzt ausrechnen? Mir fehlen ja immer noch die Schnittpunkte. (Ich sehe sie auf dem Graphen, doch wie rechne ich sie aus?)

---

Ich habe hier mit meiner Rechnung aufgehört, weil ich dachte, der Rest ist klar:

$\\x=0\quad \vee\quad x^2-4=0$

Jetzt rechnest du nur noch

$\\x=0\quad \vee\quad x^2=4\\ \\x=0\quad \vee\quad x=\sqrt{4}\\ \\x=0\quad \vee\quad x=2\quad \vee\quad x=-2$

---

Alles klar! Ich bekomme dann für die zwei Flächen jeweils 4 raus. Das zusammen ergibt 8. Ist das so richtig?

---

Ja, das ist richtig.

Answer 2

Hallo

Bei so was hilft immer eine Skizze. Dann siehst du, dass du erstmal die Schnittpunkte der 2 Funktionen brauchst. für a) stehen die da schon  da, dann musst du das Integral von  f(x)-g(x) vom linken x bis zum rechten berechnen, falls es wie bei b negativ wird den Betrag nehmen oder g-f integrieren.

also konkret für a)$$|\int \limits_{-2}^{1} (-x^2-x+2) dx|=...$$

Gruß lul

Comments

Hallo, danke für die Antwort. Ich habe dieses Thema zum ersten mal. Leider verstehe ich nicht viel von dem, was du Kommentiert hast. Könntest du mir vielleicht den Rechenweg für a) zeigen? Ich würde dann die restlichen Aufgaben alleine machen.