Berechne die Fläche zwischen den beiden Funktionsgraphen.

Question

Hallo, während meiner Prüfungsvorbereitung komme ich bei folgender Aufgabe nicht weiter und bitte um die Lösung:

Aufgabe 5 (Integralrechnung) Gegeben seien die Funktionen \( f_{1}(x)=\sin \left(\frac{\pi}{2} x\right) \) und \( f_{2}(x)=-x^{3}+6 x^{2}-8 x \). Berechnen Sie die Fläche zwischen den beiden Funktionsgraphen.

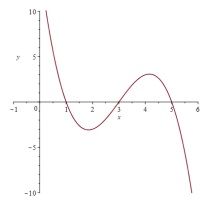
Die Schnittstellen der beiden Funktionsgraphen lauten \( x_{1}=0, x_{2}=2, x_{3}=4 \)

Vielen Dank im Voraus für die Hilfe.


Liebe Grüße

Sevi

Comments

Das Bild passt nicht zur angegebenen Funktiion.

Deine Abbildung passt zu

\( -x^{3}+9 x^{2}-23 x+15 \).

Answer 1

Hallo,

bilde die Differenz der Funktionen und integriere von Nullstelle zu Nullstelle. Addiere die Beträge der Integrale.

Das ergibt ungefähr 2•5.27324=10.54648.

Answer 2

Das gibt zwei Stücke, einmal von 0 bis 2, da rechnest du

\(   \int\limits_0^2 ( \sin \left(\frac{\pi}{2} x\right) -(-x^{3}+6 x^{2}-8 x) ) dx \)

und für das zweite Stück

\(  \int\limits_2^4 ( -x^{3}+6 x^{2}-8 x - \sin \left(\frac{\pi}{2} x\right) ) dx\)