Berechnen Sie die Innenwinkel der Laternenseiten.

Question

Eine Laterne hat die Form eines Pyramidenstumpfes mit einer quadratischen Grundfläche.

Es sind die Punkte A (5 | -5 | 0), B (5 | 5 | 0), E (2 | -2 | 15) und G (-2 | 2 | 15) (Koordinaten in cm)

a) Berechnen Sie die Innenwinkel der Laternenseiten.

b) Berechne die Spitze, die die vollständige Pyramide besitzen würde.

c) Berechne das Volumen der Laterne.

Answer 1

Hallo,

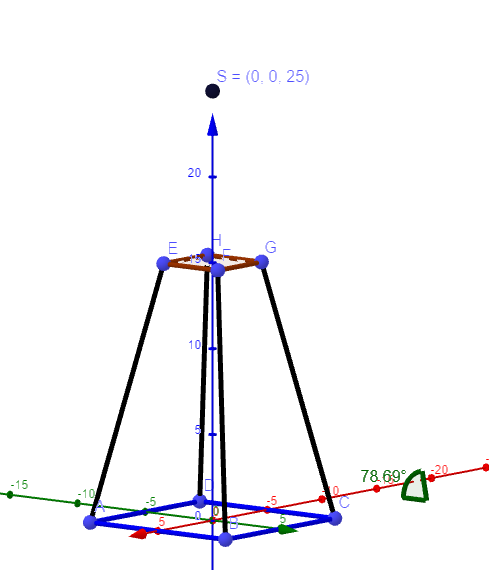
a) Berechnen Sie die Innenwinkel der Laternenseiten.

Ich gehe davon aus, dass damit die Winkel zwischen Seitenflächen und Grundfläche gemeint sind.

Schnittwinkel zwischen Ebenen können berechnet werden mit

\(cos(\alpha)=\frac{|\vec{a}\circ\vec{b}|}{|\vec{a}|\cdot|\vec{b}|}\)

Wähle für \( \vec{a} \) z.B. das Kreuzprodukt aus \( \vec{AB} \) und \( \vec{AE} \) und für \( \vec{b} \) den Normalenvektor der x₁x₂-Ebene.

b) Berechne die Spitze, die die vollständige Pyramide besitzen würde.

Berechne z.B. den Schnittpunkt der Geraden durch die Punkte A und E sowie durch B und F.

c) Berechne das Volumen der Laterne.

Verwende die Formel

\(V=\frac{1}{3}h(a^2+ab+b^2)\)

a ist die Länge der Grundseite, b die Länge der oberen Fläche.

Gruß, Silvia