Hallo,
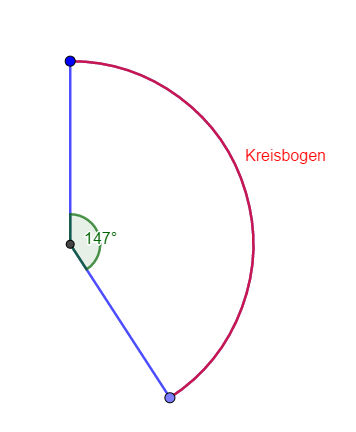
Ein Kreisausschnitt hat den Radius 4,5 cm und den Mittelpunktswinkel 147 Grad. Wie groß ist sein Flächeninhalt; Wie viel Prozent der Kreisfläche ist das?Wie lang ist der Kreisbogen?
Ein Kreisbogen ist Teil der Kreislinie eines Kreises. Seine Länge ist proportional zur Größe des zugehörigen Mittelpunktswinkels. Ist die Länge eines Kreisbogens also unbekannt, kann sie mit Hilfe des gesamten Kreisumfangs und des zum Kreisbogen gehörenden Mittelpunkswinkels berechnet werden, wenn dieser bekannt ist.
Formel zur Bestimmung der Länge eines Kreisbogens:
\(\frac{\text{Länge des Kreisbogens}}{\text{Kreisumfang}}=\frac{\text{Größe des Mittelpunktswinkels}}{\text{360\degree}}\\ \frac{b}{U}=\frac{\alpha}{360\degree}\)
mit \(U=2\cdot\pi\cdot r\)
hier: \(U=2\cdot\pi\cdot 4,5=9\pi\)
Du löst die Formel nach b auf und setzt die bekannten Größen ein:
\( b=\frac{\alpha}{360}\cdot U=\frac{147}{360}\cdot 9\pi\approx 11,55 cm\)
Für den Flächeninhalt eines Kreisausschnitts/Sektors gilt das Gleiche hinsichtlich der Proportionalität:
\(\frac{\text{Flächeninhalt des Sektors}}{\text{Flächeninhalt des Kreises}}=\frac{\text{Größe des Mittelpunkswinkels}}{360\degree}\\ \frac{A_{S}}{A_K}=\frac{\alpha}{360\degree}\)
Löse nach AS auf und berechne:
\(A_S=\frac{147}{360}\cdot 63,62=25,98cm^2\)
Wieviel Prozent 25,98 von 63,62 sind, kannst du sicherlich selbst berechnen.
Gruß, Silvia