Berechnen Sie den Flächeninhalt der Fläche, die zwischen der kleinsten und der größten Nullstelle (der Funktion

Question

Aufgabe:

Gegeben sei die folgende Funktion:
$$ f(x)=-x^{3}+7 x^{2}+x-7 $$
Berechnen Sie den Flächeninhalt der Fläche, die zwischen der kleinsten und der größten Nullstelle (der Funktion
\( f(x) \) ) zwischen der Funktion \( f(x) \) und der X-Achse liegt. Geben Sie den Flächeninhalt ungerundet und ohne Einheit
an.
Der Flächeninhalt beträgt:

Wie berechnet man die Flächeninhalt? VG

Answer 1

Hallo,

berechne zuerst die Nullstellen.

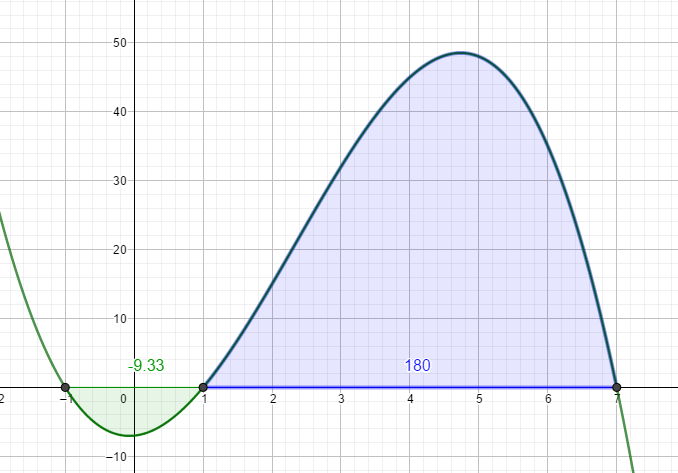
Bilde dann die Stammfunktion, berechne die einzelnen Flächeninhalte - Integral von -1 bis 1 und dann von 1 bis 7 - und addiere sie. Da der grüne Flächeninhalt unterhalb der x-Achse liegt, musst du den Betrag deines Ergebnisses nehmen und zu dem Flächeninhalt des blauen Stücks hinzuzählen.

Melde dich, falls du dazu noch Fragen hast.

Gruß, Silvia