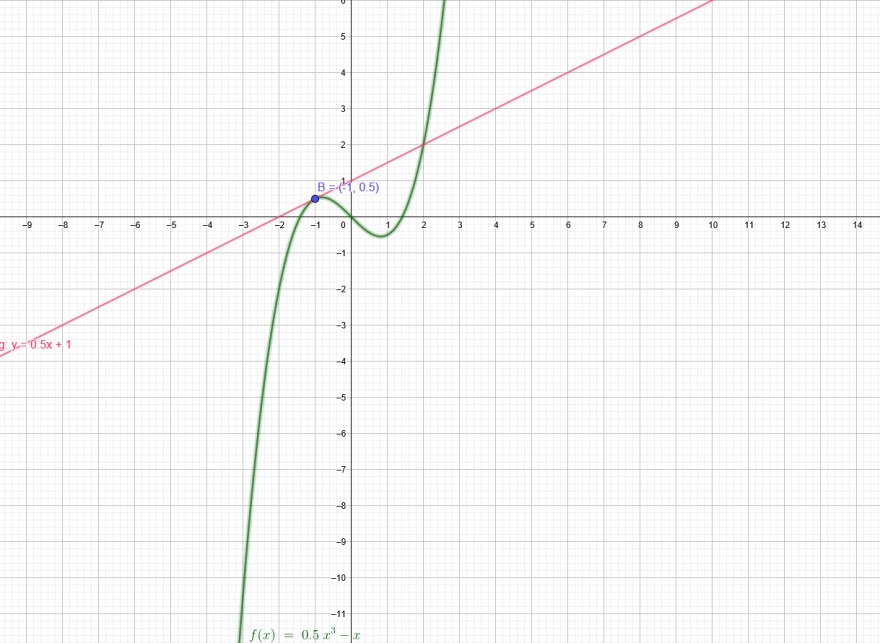
f(x)= 0,5*x³ − x
x₀= −1
f(-1)= 0,5*(-1)³ − (-1)= -0,5+1=0,5
f´(x) =0,5 *3*x^(3-1) - 1 = 1,5*x^2 - 1
x₀= −1
f´(-1)= 1,5*(-1)^2 - 1 = 0,5
B(-1| 0,5)
Punkt-Steigungsform der Geraden ( hier Tangente):
\( \frac{y-0,5}{x-(-1)} \) =0,5 → \( \frac{y-0,5}{x+1} \) =0,5 → y = 0,5 x +1