Hallo.
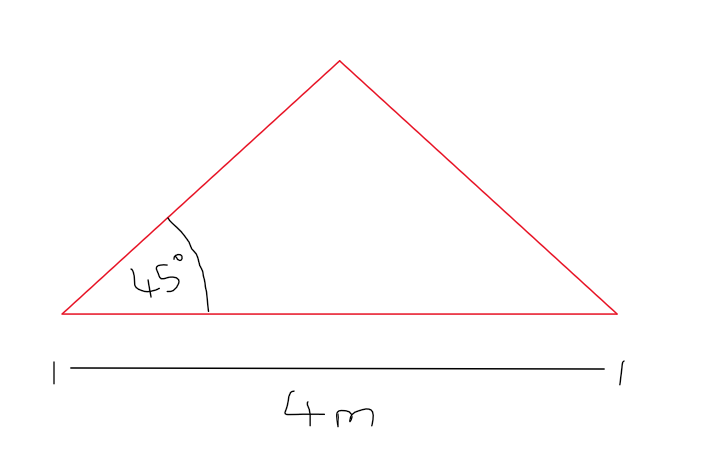
Wie ermittle ich die Höhe dieses Dreiecks, wenn ich nur den einen Winkel 45* und die untere Seitenlänge 4m habe?
Ich benötige nämlich für den weiteren Ablauf einer Aufgabe die Höhe dieses Dreiecks aber ich habe keinen Ansatz..
kann mir da jemand bitte auf die Sprünge helfen? Es ist ein gleichschenkliges Dreieck denke ich mal.
Danke
Text erkannt:
\( \frac{145^{\circ}}{4 m} \)