Der Schrank hat eine Tiefe von 60 cm.Wie breit und wie hoch muss der Schrank sein,wenn sein Rauminhalt möglichst …

Question

Aufgabe:

Unter einer Dachschräge soll ein Schrank wie in der Skizze eingebaut werden.(Schrank links beginnend im Nullpunkt ; breite 6,40 m Schnittpunkt mit de4 geraden, Höhe 3,20 m)

Der Schrank hat eine Tiefe von 60 cm.Wie breit und wie hoch muss der Schrank sein,wenn sein Rauminhalt möglichst groß sein soll?wie groß ist der maximale Rauminhalt?

Problem/Ansatz:

ich muss meiner Tochter helfen und habe keine Ahnung.

Habe schon Ansätze gefunden......

SF=b*h

h=1/2 *b+3,2

Y=-1/2x+3,2

ST=b*(-1/2*b+3,2)

Aber wirklich weiter weiß ich nicht

Comments

Unter einer Dachschräge soll ein Schrank wie in der "S k i z z e" eingebaut werden.

Diese fehlt leider.

---

Hallo,

Willkommen in der Mathelounge!

Deine Angaben sind nicht schlüssig ... Du schreibst "breite 6,40 m" und dann "Wie breit ... muss der Schrank sein".

Außerdem fehlt eine Nebenbedingung, wenn ich mal davon ausgehe, dass es sich um einen Extremwert-Aufgabe handelt. D.h. irgendetwas, was die Abmessungen des Schranks einschränkt. Sonst wird der Schrank so groß wie der ganze Raum, in dem er steht ;-)

Kannst Du die Skizze noch näher beschreiben oder besser noch abzeichnen und hier hochladen.

Answer 1

Der Leser dieser Aufgabe kann nur vermuten, was gemeint ist. Ich vermute, dass diese Ausgangslage gemeint ist:

Die Gerade, welche die Dachschräge modelliert, hat wohl die Gleichung Y=-1/2x+3,2.

Die Breite des Schrankes nenne ich x, dann ist die zugehörige Höhe -1/2x+3,2. Bei gegebener Tiefe hängt das Volumen des Schrankes nur von der grau unterlegten Fläche f(x) ab. Diese ist f(x)=x·(-1/2x+3,2). Das Maximum von f(x) (=Scheitelpunkt der Parabel oder Nullstelle der ersten Ableitung) gibt die Breite des größten Volumens an.

Answer 2

Ich vermute einmal
Funktion der Dachschräge
Y = -1/2x + 3,2
Nullpunkt
x = 6
max Fäche
Breite 6 / 2 = 3 m
Höhe 32 / 2 = 1.6 m

Stell bitte die Aufgae als abfotografierten Text
oder das Bild ein

Falls es Probleme gibt schicke mir das Bild als
e-mail Anhang an

g e o r g . h u n d e n b o r n (at) t - o n l i n e. d e

Leerzeichen entfernen

Comments

Hallo Nadine,
dein Bild ist angekommen.
Es ist so wie vermutet.
Allerdings ist der Nullpunkt bei
6,4 / 2 = 3.2 m

Die Fläche des Schranks ergibt sich aus

untere Breite ( x ) mal ( Höhe = -1/2 * x + 3.2.)
A ( x ) = x * ( -1/2 * x + 32.)
A ( x ) = -1/2 * x^2 + 3.2 * x
Nun benötigt man die Differentalrechnung
um das Maximum der Fläche festzustellen
1.Ableitung
A ´( x ) = -1 * x + 3.2
Maximum
-1 * x + 3.2 = 0
x = 3,2 m

Die Höhe ergibt sich
h ( x ) = -1/2 * x + 3.2
h ( 3.2 ) = - 1/2 * 32 + 3.2 = 1.6 m

Fläche
A = 3.2 * 1.6 = 5.12 m^2

das Volumen zu
5.12 * 0.6 = 3.072 m^3

mfg Georg

---

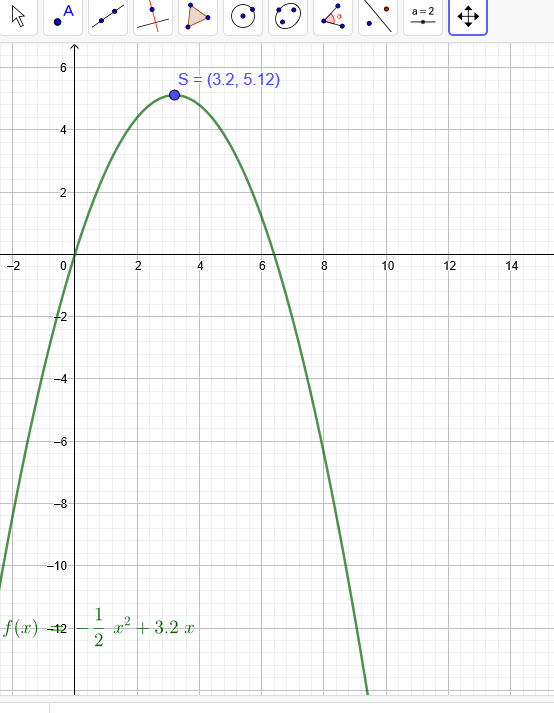
Ohne Ableitung geht es so:

A ( x ) = -\( \frac{1}{2} \) * x^2 + 3,2 * x

-\( \frac{1}{2} \) * x^2 + 3,2 * x=0

x*( - \( \frac{1}{2} \) * x+3,2) = 0

x₁=0

x₂=6,4

Nun liegt der Extremwert bei einer Parabel 2. Grades in der Mitte zwischen den beiden Nullstellen.

x_S= \( \frac{0+6,4}{2} \) = 3,2

A ( 3,2 ) = -\( \frac{1}{2} \) * 3,2^2 + 3,2 *3,2=5,12

---

A ( x ) = - 1 / 2 * x^2 + 3,2 * x
Also nur die Scheitelpunktform bestimmen
A ( x ) = - 1 / 2 * ( x^2 - 6.4 * x )
A ( x ) = - 1 / 2 * ( x^2 - 6.4 * x + 3,2^2 - 3,2^2 )
A ( x ) = - 1 / 2 * ( x^2 - 6.4 * x + 3,2^2  ) + 3.2^2 / 2
A ( x ) = - 1 / 2 * ( x - 3,2  ) ^2 + 3.2^2 / 2
A ( x ) = - 1 / 2 * ( x - 3,2  ) ^2 + 5.12

Der Scheitelpunkt der Flächenfunktion ist bei
S ( 3.2 m | 5,12 m^2 )

Wenn man Differtialrechnung kann würde ich diese
auf jeden Fall bevorzugen: