\(z=r\cdot e^{i\phi} ; \bar{z}=r\cdot e^{-i\phi} \)
\(z^5=r^5\cdot e^{i\cdot5\phi} ; \bar{z}=r\cdot e^{-i\phi} \)
\(r^5\cdot e^{i\cdot5\phi}=r\cdot e^{-i\phi} \)
\(r^5=r ; 5\phi=n\cdot2\pi-\phi ; n\in\mathbb N\)
\(r=0\Rightarrow z_0=0\)
oder
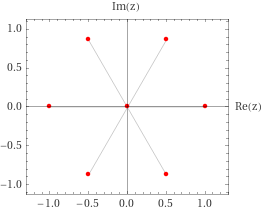
\(r=1 ; 6\phi=n\cdot2\pi; n\in\mathbb N \)
\(z_k=e^{i\cdot k\phi/3}; k=1; ... ; 6\)