Text erkannt:
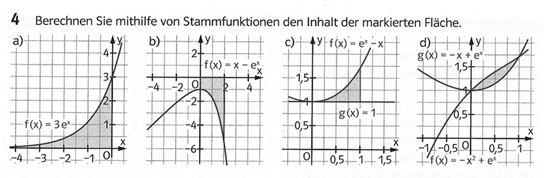
4 Berechnen Sie mithilfe von Stammfunktionen den Inhalt der markierten FIäche
Großbuchstaben = Stammfunktion
Habe alle Stammfunktionen noch mal gerechnet es tut mir leid aber ich finde den Fehler nicht bitte helf mir. Ich stehe gerade echt auf dem Schlauch.
4a) F(x)= 3e^x A=2^2/2-e^2(^0^2/2)=4,39
4b) F(x)= x^2/2-e^x A=2^2/2-e^2-(0^2/2-e^0)=4,39
4c) G(x)=x F(x)=e^x-x^2/2 A=1+e^1-1/2-(e^0-0^2/2)=2,21828
4d) F(x)= -x^3/3+e^x G(x)=-x^2/2+e^x
A= -1^3/3+e^1-(0^3/3+e^0)+((-1^2/2+e^1-(0^2/2+e^0)=2,6