Hallo,
Willkommen in der Mathelounge!
zunächst mal ist das nicht der Fall, dass bei einer Lösung \((x_0;\,y_0)\) der diophantischen Gleichung $$ax + by = c$$immer eine der beiden Zahlen negativ ist. Ein einfaches Gegenbeispiel ist $$3x+ 5 y = 11$$Hier ist \((2;\, 1)\) eine Lösung dieser Gleichung und beide Zahlen sind positiv.
Du fragtest aber
... die durch den euklidischen Algorithmus gefunden wird. ...
Der erweiterte euklidische Algorithmus liefert zunächst die Lösung für \(ax' + by' = 1\). Ist hier eine Lösung für \((x'_0;\,y'_0)\) gefunden, so ist eine Lösung für \(ax + by = c\) schlicht $$(x_0;\,y_0) = (x'_0\cdot c;\, y'_0 \cdot c)$$Und bei der Lösung zu $$ax' + by' = 1$$muss zwangsläufig eine der beiden Zahlen \(x'\) oder \(y'\) negativ sein, wenn \(a\) oder \(b\) größer als \(1\) ist, was praktisch immer der Fall ist.
Nehmen wir das Beispiel von oben$$3x' + 5y' = 1 \implies (x_0';\, y_0') = (2;\, -1)$$Wieder ist eine der beiden Zahlen negativ und nach dem Vorgehen oben wäre nun$$(x_0;\, y_0) = (11x_0';\, 11y_0') = (22;\,-11)$$Das ist die Lösung, die Dir der übliche Lösungsweg liefern würde. Und hier ist tatsächlich prakisch immer eine der beiden Zahlen des Lösungspaar negativ. Daran ändert die Multiplikation mit \(c\) rein gar nichts.
Das ist aber nicht die einzige Lösung, denn mit dem Vielfachen der Lösung von folgender Gleichung$$3 u + 5 v = 0 \implies (u;\,v) = (-5;\,3)$$kann man eine gefundene Lösung addieren und bekommt eine neue. Hier ganz konkret$$(22;\, -11) + 4 \cdot (-5;\,3) = (22 - 4\cdot 5;\, -11 + 4\cdot 3) = (2;\,1)$$Zwei positive Zahen erhält man nur dann, wenn das \(c\) ausreichend groß ist, und die beiden Koeffizienten \(a\) und \(b\) 'passen'.
Das stellt man sich am besten graphisch vor. Die Gleichung \(ax+by = c\) beschreibt auch eine Gerade in der Ebene, deren Normalenvektor in Richtung des ersten Quadranten verläuft. Für unser Beispiel:
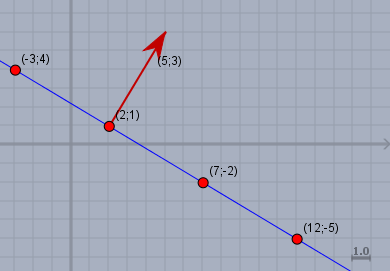
Die Lösungen sind die Punkte, an denen die Gerade ganzzahlige Koordinaten hat. Da die Gerade aber immer einen Normalenvektor besitzt, der im ersten Quadranten liegt, durchquert die Gerade im wesentlichen den 2. und 4. Quadranten. Und dort ist immer genau eine der Koordinaten negativ.
Die Lösung \((2;\,1)\) ist in unserem Beispiel offensichtlich auch die einzige, bei der das nicht so ist.