Monotonie bei Wurzelfunktionen (allgemein)

Question

bei der Monotonie von Wurzelfunktionen:

Wie geht man dort vor? Ich hatte in meiner vorherigen Frage die Funktion

$$f(x) =\sqrt{-x^2-3x-2}$$ mit -2<x<-1/2 (Bereich so in der Aufgabenstellung gegeben), bei der mir keiner wirklich weiterhelfen konnte.

Wie geh ich hier bzw. allgemein bei Wurzelfunktionen vor?

Monotonie ist ja f'(x) > bzw. < 0, aber wie mache ich das halt bei Wurzelfunktionen. Muss ich nur die innere Funktion betrachten? Die gesamte Funktion? Was ist wichtig?

Danke für die Hilfe.

Answer 1

bei der mir keiner wirklich weiterhelfen konnte.

Ich hoffe doch ich habe dir eine zufriedenstellende
Anwort geben können.

Kurzhinweis : gilt bei jeder Funktion
f ( x ) = ...
1 Ableitung bilden
f ´( x ) = ...

Ermitteln wann die Funktion
< 0 ( negativer Wert, fallend )
= 0 ( Extrempunkt, Sattelpunkt, weder fallend noch steigend )
> 0 ( positiver Wert, steigend )
ist.

Gern rechne ich dir noch ein Beispiel vor,
Du sollst nicht unwissend sterben.

mfg Georg

Comments

Danke Georg, so war das auch gar nicht gemeint. Ich dachte nur, dass da keine Antwort mehr von dir kommt, sodass ich nach weiterer Hilfe gesucht habe.

Wenn ich also eine kritische Stelle (f'(x) = 0 finde, ist die Funktion automatisch nicht mehr monoton?
Ich glaube nämlich doch...sollte es nämlich eine Sattelstelle sein, könnte die Funktion ja dann trotzdem wieder steigen, oder irre ich mich?

Sprich wenn ich bei der Funktion von vorhin weiß, dass x=-1,5 eine Extremalstelle ist, muss ich dann noch gucken wie Werte "links" und "rechts" von -1,5 sind um dann sagen zu können ob die Funktion monoton ist bzw. ob sie monoton fallend/steigend ist, oder?

Vielen Dank dir für deine Hilfe :)

---

siehe deine andere Frage.
Frag nach bis alles klar ist.

Answer 2

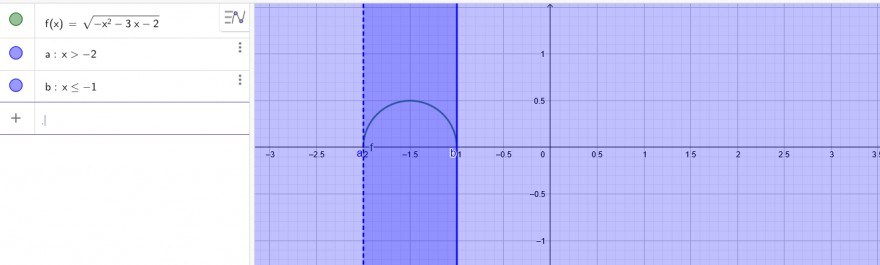
\(f(x) =\sqrt{-x^2-3x-2}\)

Nullstellen:

-x^2-3x-2 = 0

x₁=-2  ist nicht mehr im Bereich  -2<x<-1/2  somit auch keine kleineren Werte als -2

x₂=-1 ist im Bereich -2<x<-1/2 

x= - 0,9

\(f(-0,9) =\sqrt{-(-0,9)^2-3*(-0,9)-2}\)=\( \sqrt{-0,11} \) ist eine Lösung in ℂ

Somit ist der Definitionsbereich ( - 2 < x ≤ - 1]

(-x^2-3x-2)^1/2=-0,1|^2

-x^2-3x-2= 0,01

x^2+3x+2=-2, 01 Lösungen in ℂ      Wertebereich y≥0       wie weit hängt vom Extremwert ab.

Text erkannt:

\( f(x)=\sqrt{-x^{2}-3 x-2} \)
\( f^{-}(x)=\frac{-2 x-3}{2 \cdot \sqrt{-x^{2}-3 x-2}} \)
\( \frac{-2 x-3}{2 \cdot \sqrt{-x^{2}-3 x-2}}=0 \)
\( x=-\frac{3}{2} \)
\( f\left(-\frac{3}{2}\right)=\sqrt{-\left(-\frac{3}{2}\right)^{2}-3 \cdot\left(-\frac{3}{2}\right)-2}=0,5 \)
\( f^{\cdots}\left(-\frac{3}{2}\right)<0 \) somit Maximum
\( f(x) \) ist somit im Bereich \( (-2 \) bis zum Maximum steigend und vom Maximum bis \( x \leq-1 \) fallend.

Answer 3

Ist $$ f(x) = \sqrt{-x^2-3x-2} \quad\text{mit}\quad -2 < x < -1/2 $$ monoton?

Überprüfe mal die Angaben. Muss es statt "-1/2" nicht vielleicht "-3/2" oder "-1.5" heißen? Die angegebene Funktion ist höchstens für \(-2 \le x \le -1\) definiert. Vielleicht stimmt auch die Funktion nicht.

Jedenfalls lässt sich leicht einsehen, dass der Graph von f der obere Halbkreis um \((-1.5\vert 0)\) mit Radius \(0.5\) ist. Der ist streng monoton steigend für \(-2 \le x \le -1.5\) und streng monoton fallend für \(-1.5 \le x \le -1\).