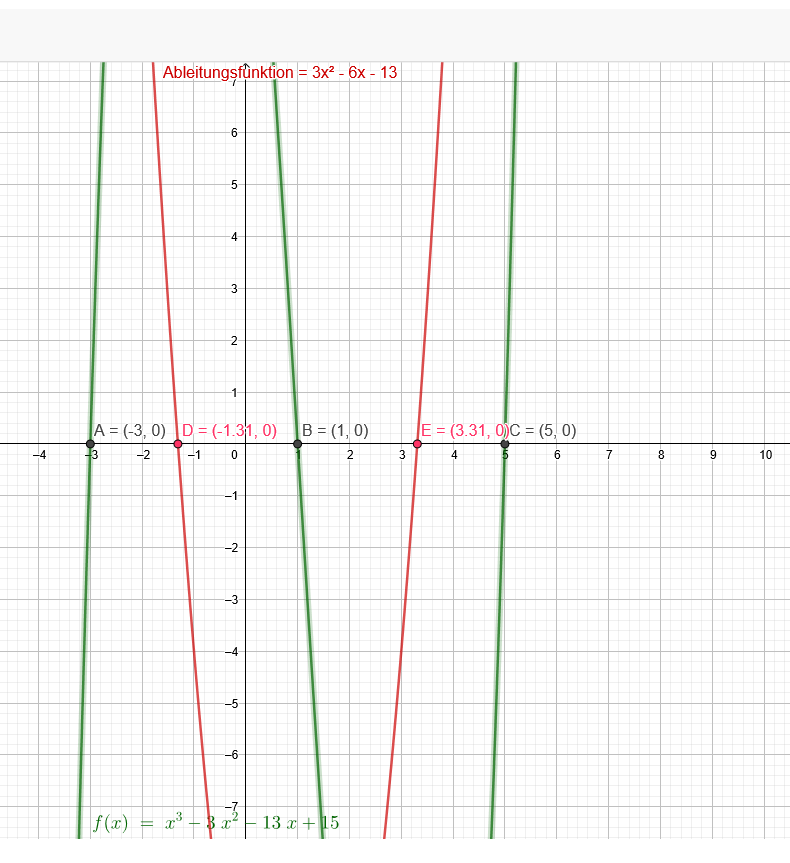
a) f(x) = x^3 - 3x^2 - 13x + 15
f´(x) = 3x^2 - 6x - 13
Extrempunkte:
3x^2 - 6x - 13=0
x^2-2x=\( \frac{13}{3} \)
(x-1)^2=\( \frac{13}{3} \)+1^2= \( \frac{16}{3} \) | \( \sqrt{} \)
x₁=1+\( \frac{4}{3} \)* \( \sqrt{3} \) ≈ 3,31 →y_1= -\( \frac{128}{9} \)*\( \sqrt{3} \)
x₂=1-\( \frac{4}{3} \)* \( \sqrt{3} \)≈ -1,31 →y_2=\( \frac{128}{9} \)*\( \sqrt{3} \)
Monotonie kann sich nur an Nullstellen der ersten Ableitung ändern.
f´(-2)=3*(-2)^2 - 6*(-2) - 13=11>0 Somit ist f(x) monoton steigend im Intervall (-∞;-1,31]
f´(3)=3*(3)^2 - 6*(3) - 13=-4 <0 Somit ist f(x) monoton fallend im Intervall [-1,31;3,31]
f´(4)=3*(4)^2 - 6*(4) - 13= 11 >0 Somit ist f(x) monoton steigend im Intervall [3,31; ∞ )