irgendwie steh ich grad am Schlauch beim Aufstellen der Zielfunktion. Vielleicht kann mir hier jemand weiterhelfen.
Aufgabe:
In einer Betriebsabteilung ist auf drei Maschinen am M1, M2, M3 eine noch unbestimmte Anzahl von jeder der Werkstücksarten E1 und E2 zu bearbeiten. Gegeben sind die Bearbeitungszeiten jedes Werkstücks auf jeder Maschine in Stunden pro Werkstück und der Zeitfonds jeder Maschine in Stunden. Wie viele Stücke E1 und E2 sind zu bearbeiten, damit der Gesamtzeitfonds maximal ausgelastet wird?
(Aufgabe: mathematisches Modell soll aufgestellt werden)
Siege Bild unten.
Problem/Ansatz:
Um die Zielfunktion z aufzustellen, würde ich einfach die Zeiten, die E1 bzw. E2 auf den Maschinen braucht, aufsummieren oder wie wäre hier der Ansatz? Übersehe ich etwas?
Mit: x1 - E1 und x2 - E2
z = 40x1 + 50x2 —> max.
NB:
10x1 + 10x2 <= 8000
10x1 + 30x2 <= 18000
20x1 + 10x2 <= 14000
NNB: x1 , x2 >= 0
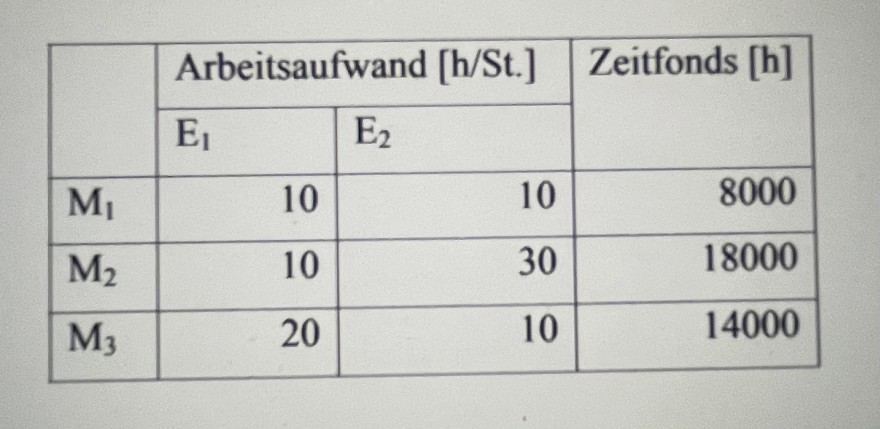
Text erkannt:
\begin{tabular}{|l|r|r|r|}
\hline \multirow{2}{*} {} & \multicolumn{2}{|l|} { Arbeitsaufwand [h/St.] } & \multirow{2}{*} { Zeitfonds [h] } \\
\cline { 2 - 3 } & \( \mathrm{E}_{1} \) & \( \mathrm{E}_{2} \) & & \\
\hline \( \mathrm{M}_{1} \) & 10 & 10 & 8000 \\
\hline \( \mathrm{M}_{2} \) & 10 & 30 & 18000 \\
\hline \( \mathrm{M}_{3} \) & 20 & 10 & 14000 \\
\hline
\end{tabular}