Gebe die Zielfunktion des dualen Programms und die Nebenbedingungen an.

Question

Aufgabe:

Gegeben sei das lineare Programm:

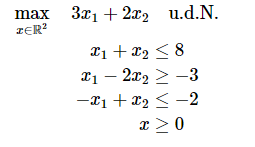
Text erkannt:

\( \begin{aligned} \max _{x \in \mathbb{R}^{2}} \quad 3 x_{1}+2 x_{2} & \text { u.d.N. } \\ x_{1}+x_{2} & \leq 8 \\ x_{1}-2 x_{2} & \geq-3 \\-x_{1}+x_{2} & \leq-2 \\ x & \geq 0 \end{aligned} \)

Gebe die Zielfunktion des dualen Programms und die Nebenbedingungen an.

Problem/Ansatz:

Ich habe die Zielfunktion \(8y_1+3y_2-2y_3\) und die Nebenbedingungen: \(y_1-y_2-y_3 \geq 3\) und \(y_1+2y_2+y_3 \geq 2\) herausbekommen. Kann das jemand bestätigen bzw. die Fehler aufzeigen?

Answer 1

Wo soll ich die Fehler suchen?

guckst du https://www.geogebra.org/m/nh4JwT7a

Ausgehend (2 angepasst) von

{x1+x2<=8,-x1+2 x2<=3,-x1+x2<=-2,3*x1+2*x2=0}

erhalte ich

\(Tablo \, :=  \, \left\{ x1 - x2 - x3 >= 3, x1 + 2 \; x2 + x3 >= 2, -8 \; x1 - 3 \; x2 + 2 \; x3 = 0 \right\} \)

sieht doch gut aus,oder?