Es gibt Funktionen, deren Gleichungen für verschiedene Bereiche von x unterschiedlich definiert sind. Fig. 3 zeigt die zusammengesetzte Funktion f mit
f(x)= -0,25(x+1)^2+2 für x < -1 und
f(x) =(x+1)^2+2 für x ≥ -1
a) Begründen Sie: f ist differenzierbar an der Stelle x0= -1. Ziehen Sie dafür sowohl Ihr Wissen über rechnerische als auch das über geometrische Methoden heran.
b) Zeichnen Sie selbst zusammengesetzte Funktionen in ein bzw. verschiedene Koordinatensysteme (Funktionsgleichungen anzugeben ist hier nicht nötig.). Wählen Sie Beispiele, die differenzierbar sind, und solche, die es nicht sind. Erklären Sie jeweils kurz dazu, warum sie differenzierbar sind oder eben nicht.
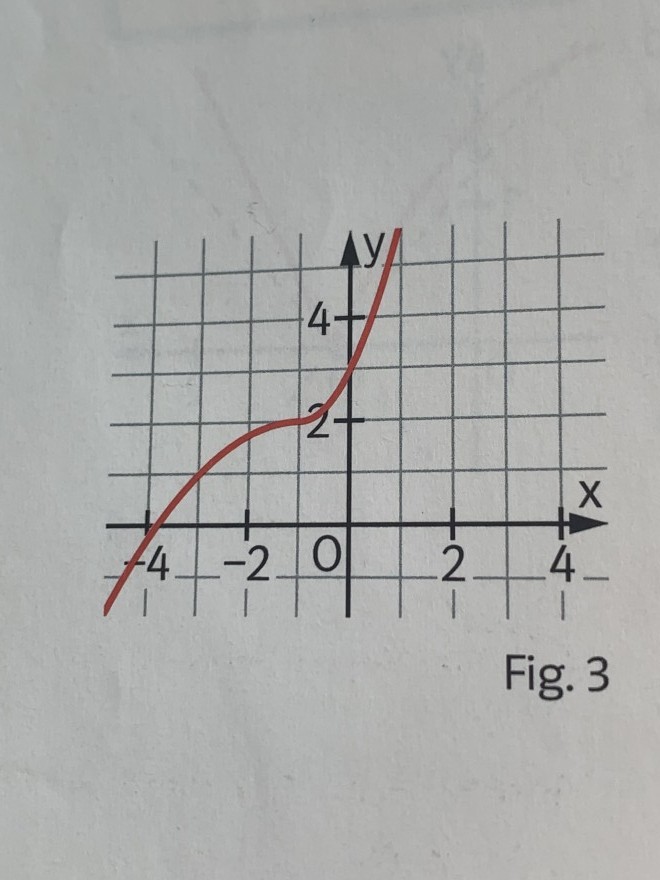 I
I