Hallo,
Willkommen in der Mathelounge!
Mache Dir zunöchst eine Zeichnung
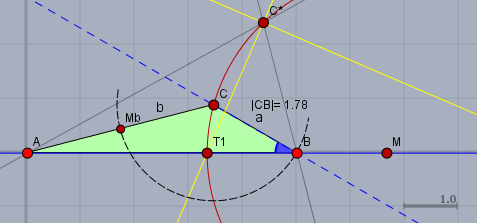
vielleicht nicht so überladen wie oben, aber wenigstens eine Skizze. Wenn \(a/b=1/2\) ist, dann ist doch \(b = 2a\). Und wenn man dann den Cosinussatz zum Winkel \(\beta\) aufstellt$$b^2 = 5^2 + a^2 - 2\cdot 5\cdot a \cos 30°$$und für \(b\) das \(2a\) (s.o.) einsetzt$$4a^2 = 5^2 + a^2 - 2\cdot 5\cdot a \cos 30°$$bekommt man eine quadratische Gleichung$$\begin{aligned} 3a^2 + 10\cos 30°\cdot a - 25 &= 0 &&|\, \div 3 \\ a^2 + \frac 53\sqrt 3\,a - \frac{25}3 &= 0 \\ a_{1,2} &= - \frac 56 \sqrt 3\,\pm \sqrt{\frac{25}{12} + \frac{25}3} \\&= -\frac56\sqrt 3\, \pm \frac 52\sqrt{\frac 53}\end{aligned}$$Die negative Lösung lassen wir weg und \(a \approx 1,78\). \(b\) ist das doppelte und die restlichen Winkel bekommst Du über den Sinussatz.
Falls Du noch Fragen hast, so melde Dich bitte.