Extremwertaufgabe kürzester weg

Question

Aufgabe: Extremwertaufgabe

Der weg soll minimal sein.

Ich bin im Ursprung (0|0) und muss zum punkt (8|-1). Auf dem weg muss ich an der geraden y=-3 vorbei. Wie berechnet man das?

Answer 1

Hallo,

Der Weg soll vom Ursprung \(O\) über einen Punkt \(X(x|\,-3)\) auf der Geraden \(y=-3\) zum Punkt \(P(8|\,-1)\) führen. Man denke sich einen Punkt \(P'\), der das Spiegelbild von \(P\) an der Geraden \(y=-3\) ist.

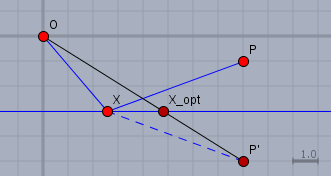
Der Weg von \(X\) nach \(P'\) ist in jedem Fall genauso lang, wie der Weg von \(X\) nach \(P\). $$|XP'| = |XP|$$Hat man also den kürzesten Weg von \(O\) über \(X\) nach \(P'\) gefunden, so ist der Punkt \(X\) der gleiche Punkt, der auch den kürzesten Weg über \(X\) nach \(P\) beschreibt.

Und dieses \(X\) liegt auf einer Geraden von \(O\) nach \(P'(8|\,-5)\)! Die Gerade durch \(O\) und \(P'\) ist$$y = -\frac 58 x$$und für \(y=-3\) ergibt sich dann$$-3 = -\frac 58 x_{opt} \implies x_{opt}= \frac{24}{5} = 4,8$$

Answer 2

Wenn ich dich richtig verstehe, sollst du also von (0|0) erst zu einem Punkt (a|.3) gehen und dann von dort zu (8|-1)?

Dieser zusammengesetzte Weg hat die Länge \( \sqrt{a^2+3^2} \)+\( \sqrt{(8-a)^2+(-1-3)^2} \).

Minimiere diese Wurzelsumme!