Gegeben ist die Funktion f(x) )= 0.5 x - 2. Eine Gerade verläuft zum Graphen von f verläuft durch den Punkt P (2|3). Eine weitere Parallele durch den Punkt (-2|-4).
a) Skizzieren Sie mit Hilfe eines Lineals den Sachverhalt.
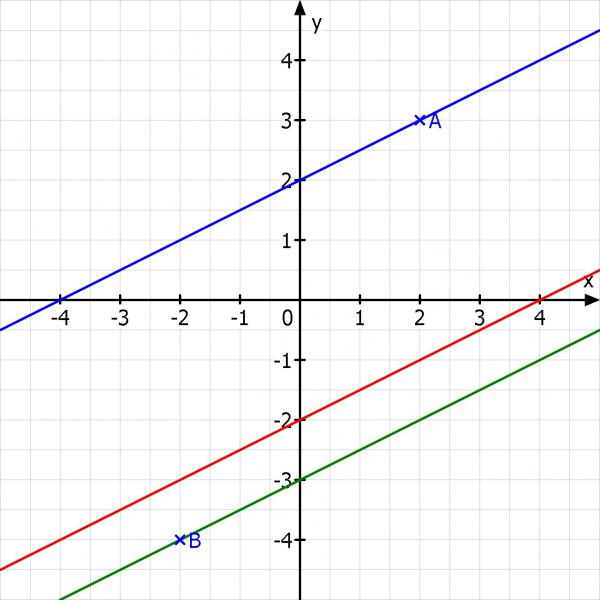
b) Bestimmen Sie die Funktionsterme der beiden Parallelen
Unsere Funktion f hat die Steigung m = 0,5, weil das der Faktor vor dem x ist.
Wir können sehr leicht eine lineare Funktionsgleichung in der Punkt-Steigungs-Form aufstellen, wenn der Graph die Steigung m hat und durch einen Punkt P(Px | Py) geht.
g1(x) = m * (x - Px) + Py = 0,5 * (x - 2) + 3
Ausmultiplizieren ergibt:
g1(x) = 0,5 * (x - 2) + 3 = 0,5x - 1 + 3 = 0,5x + 2
g2(x) = m * (x - Px) + Py = 0,5 * (x - (-2)) - 4
Ausmultiplizieren ergibt:
g2(x) = 0,5 * (x - (-2)) - 4 = 0,5 * (x + 2) - 4 = 0,5x + 1 - 4 = 0,5x - 3
c) Berechnen Sie die Schnittpunkte der beiden Parallelen mit den Koordinatenachsen
Schnittpunkt mit der Y-Achse
g1(0) = 0,5*0 + 2 = 2
g2(0) = 0,5*0 - 3 = -3
Schnittpunkt mit der x-Achse
g1(x) = 0
0,5x + 2 = 0
0,5x = -2
x = -2/0,5 = -4
g2(x) = 0
0,5x - 3 = 0
0,5x = 3
x = 3/0,5 = 6