welche maße sollte der grundriss haben?

Question

Aufgabe:

Auf einer dreieckigen Wiese soll ein Gebäude mit rechteckigem Grundriss so gebaut werden, dass es direkt an der Schlossallee und die Parkstraße grenzt. Die Schlossallee ist 120m lang und die parkallee ist 60m lang. die verbleibenden Dreieckesollen als grünfläche genutzt werden. welche maße sollte der grundriss haben?

das ganze soll wieder als quadratische funktion dargestellt werden.

Problem/Ansatz:

Könnte mir bitte bitte jemand mit dem lösungsweg helfen? Ich weiß nicht wie ich da ran gehen kann

Answer 1

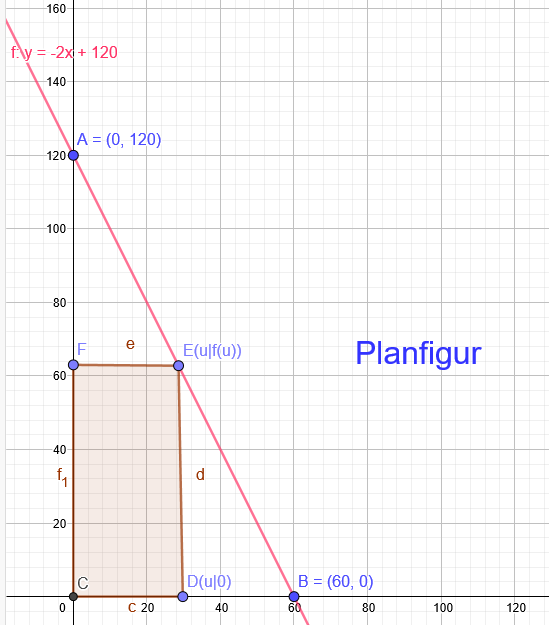
Ich nehme an, dass das Gebäude maximal sein soll:

HB:     A(u)=u*f(u)   soll maximal werden.

NB:      f(u)=  -2u+120

A(u)=u*(-2u+120 )=-2u^2+120u

\( \frac{d A(u) }{du} \)=-4u+120

\( \frac{d A(u) }{du} \)=0

-4u+120=0

u=30             f(30)  =  (-2*(30)+120 ) = 60

(\( \frac{d A(u) }{du} \))´= - 4 < 0 → Maximum

A(30)=-2*(30)^2+120*(30)

A_max =1800\( m^{2} \)