Aufgabe:Gesucht ist der Inhalt derjenigen Fläche A, die von den Graphen der Funktionen f und g sowie der y-Achse begrenzt wird. Fertigen Sie zunächst eine Grobskizze an.
f(x)=\( \frac{1}{4} \)*(\( e^{x} \)-1)
g(x)=2-\( e^{x} \)
Wie groß ist die auszurechnende Fläche A?
Problem/Ansatz:
Ich habe bereits die Schnittstelle berechnet und bin auf ln(1,8)≈ 0,59 gekommen.
Anschließend habe ich f(x) von g(x) abgezogen und habe die Differenzfunktion d(x) = \( \frac{5*e^{x}}{4} \)-\( \frac{9}{4} \) herausgefunden.
Von dieser habe ich anschließend die Stammfunktion gebildet:
D(x) =\(\frac{5*e^{x}}{4}\)-\( \frac{9}{4} \)x heraus
Dort setze ich nun 0,59 und 0 ein. Leider komme ich jedoch dabei auf - 0,32 und das haut nicht hin.
Ich würde mich über Hilfe freuen. 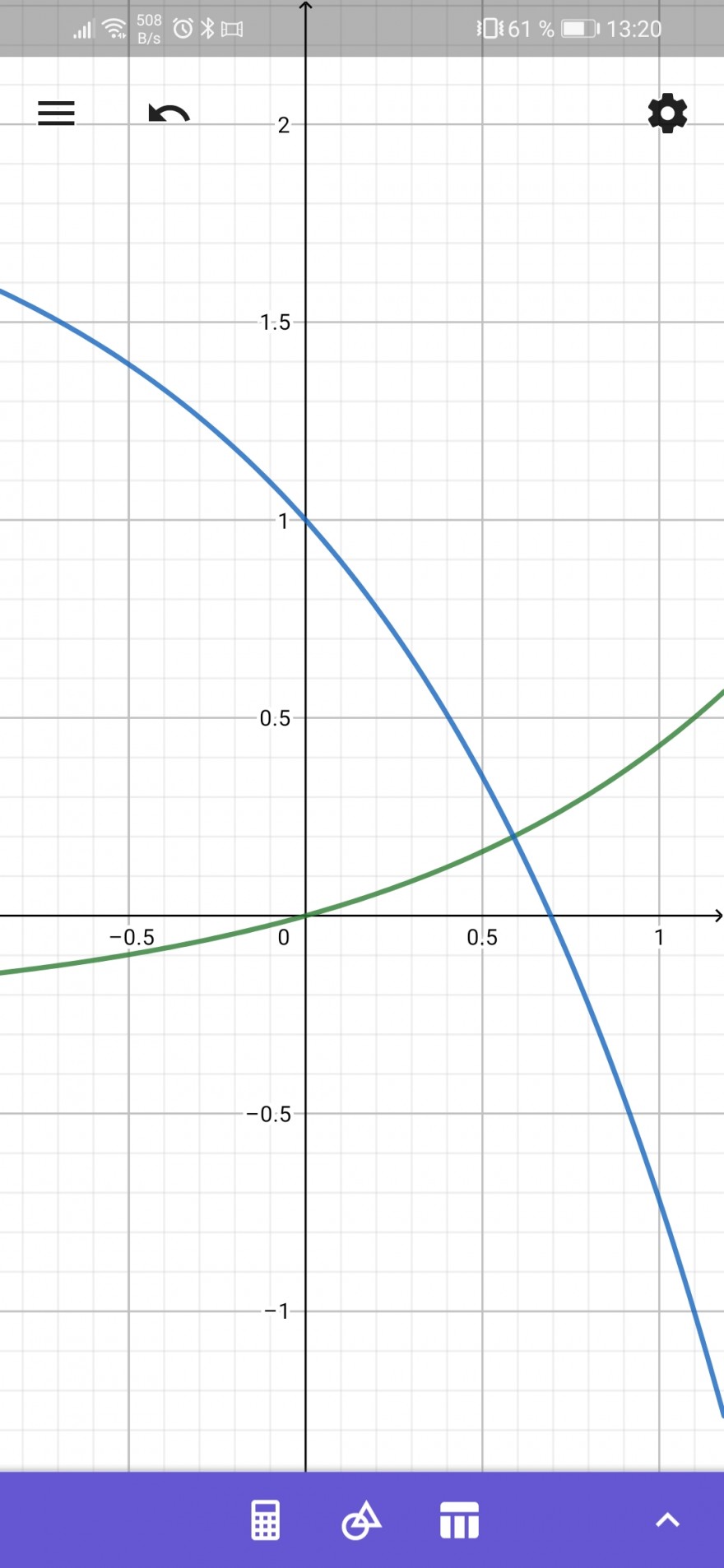
Text erkannt:
16
\( A \)