Begründe: Die Funktion f: x → 3x² - 5 mit der Definitionsmenge ℝ ist nicht umkehrbar.

Question

Problem/Ansatz:

a) Begründe: Die Funktion f: x → 3x² - 5 mit der Definitionsmenge ℝ ist nicht umkehrbar.
b) Ist die Funktion f: x → 3x² - 5 für x ≥ 0 umkehrbar? Gib in diesem Fall die Gleichung der Umkehrfunktion an und skizziere beide Graphen.

Answer 1

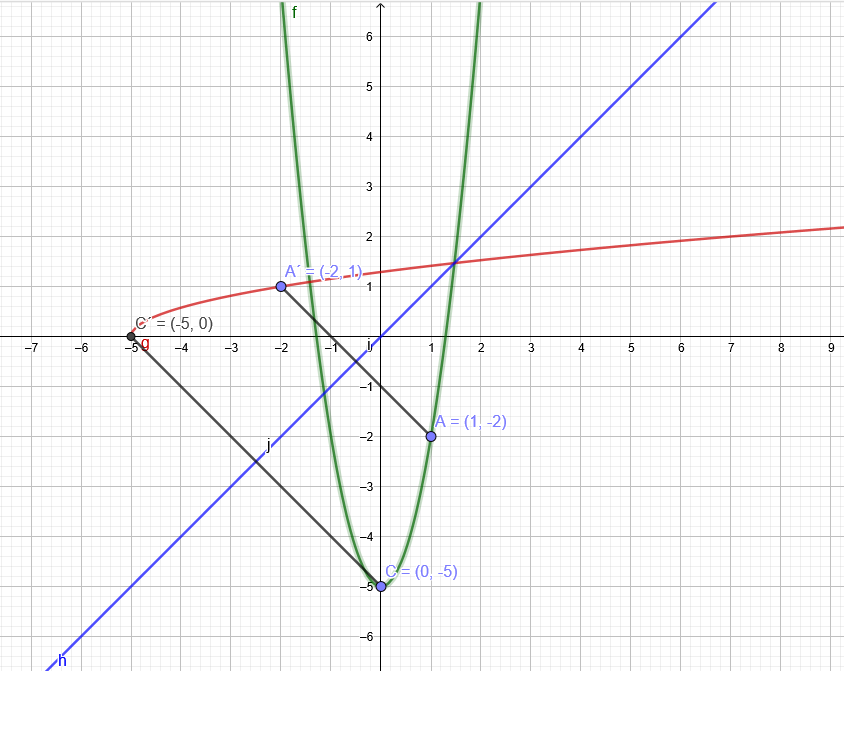
y=3x^2-5

Umkehrfunktion:

x,y Tausch

x=3y^2-5

3y^2=x+5

y^2=\( \frac{x+5}{3} \)

Text erkannt:

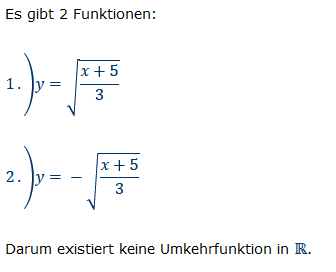
Es gibt 2 Funktionen:
1.) \( y=\sqrt{\frac{x+5}{3}} \)
2.) \( y=-\sqrt{\frac{x+5}{3}} \)
Darum existiert keine Umkehrfunktion in \( \mathbb{R} \).

b) f(x)=3x² - 5 für x ≥ 0   Hierfür existiert eine Umkehrfunktion siehe 1.)

Comments

Vielen Dank!

Answer 2

Auf R ist f(x) nicht bijektiv und damit nicht umkehrbar.

f(x) = f(-x)