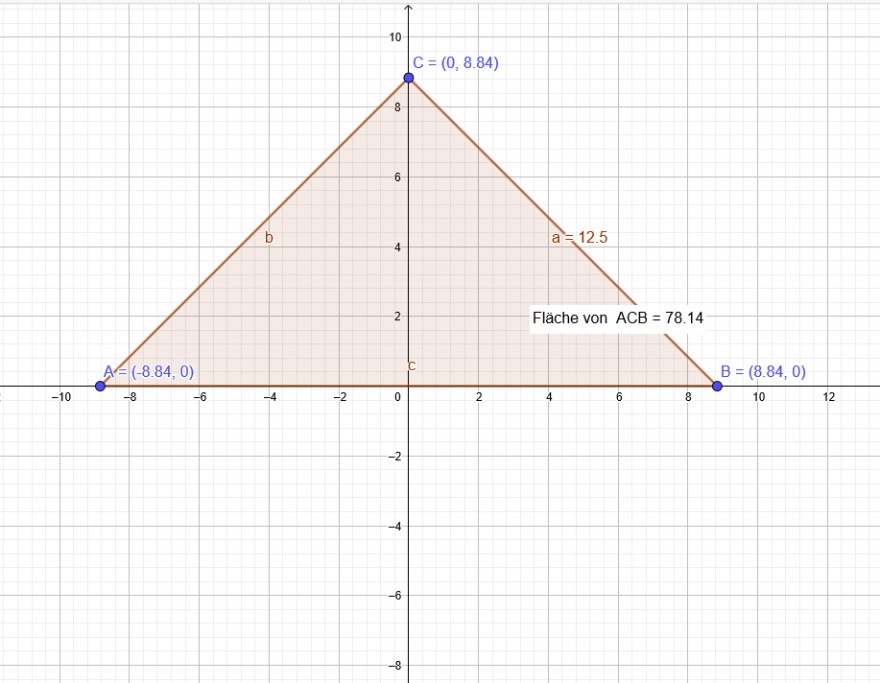
Querschnitt : oben offenes gleichschenkliges Dreieck:
Schenkellänge: 12,5 cm Höhe und Breite variabel
HB: A(h,b)=\( \frac{h*b}{2} \) soll maximal werden.
NB: h^2+ (\( \frac{b}{2} \))^2 = 12,5^2 → h^2=12,5^2-(\( \frac{b}{2} \))^2→ h = (12,5^2-(\( \frac{b}{2} \))^2)^0,5
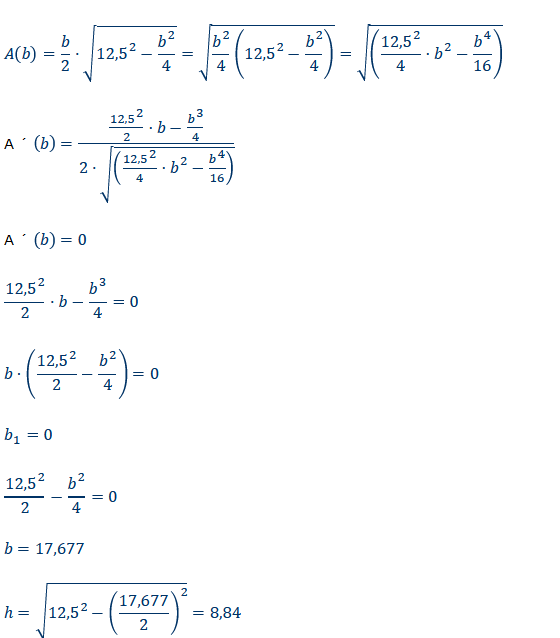
Text erkannt:
\begin{tabular}{l}
\( A(b)=\frac{b}{2} \cdot \sqrt{12,5^{2}-\frac{b^{2}}{4}}=\sqrt{\frac{b^{2}}{4}\left(12,5^{2}-\frac{b^{2}}{4}\right)}=\sqrt{\left(\frac{12,5^{2}}{4} \cdot b^{2}-\frac{b^{4}}{16}\right)} \) \\
\( A^{\prime}(b)=\frac{\frac{12,5^{2}}{2} \cdot b-\frac{b^{3}}{4}}{2 \cdot \sqrt{\left(\frac{12,5^{2}}{4} \cdot b^{2}-\frac{b^{4}}{16}\right)}} \) \\
\( A \cdot(b)=0 \) \\
\( b \cdot\left(\frac{12,5^{2}}{2}-\frac{b^{2}}{4}\right)=0 \) \\
\( b_{1}=0 \) \\
\( \frac{12,5^{2}}{2} \cdot b-\frac{b^{3}}{4}=0 \) \\
\( \frac{12,5^{2}}{2}-\frac{b^{2}}{4}=0 \) \\
\( b=17,677 \) \\
\hline \( 12,5^{2}-\left(\frac{17,677}{2}\right)^{2}=8,84 \)
\end{tabular}