b und c gilt es zu erarbeiten

Question

Aufgabe:

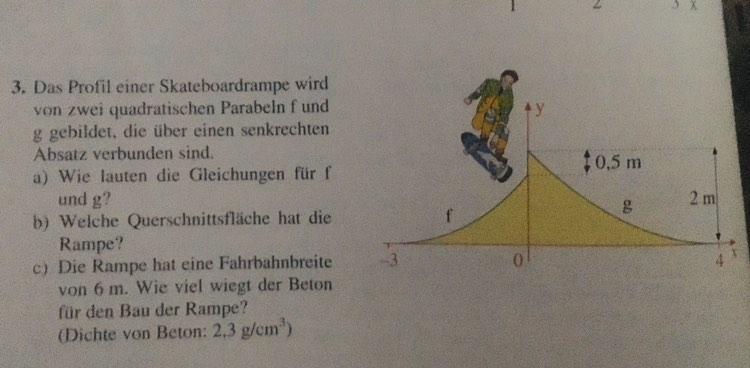
Text erkannt:

3. Das Profil einer Skateboardrampe wird von zwei quadratischen Parabeln \( \mathrm{f} \) und g gebildet, die über einen senkrechten Absatz verbunden sind.

b) Welche Querschnittsfláche hat die Rampe?
c) Die Rampe hat eine Fahrbahnbreite von \( 6 \mathrm{~m} \). Wie viel wiegt der Beton fur den Bau der Rampe? (Dichte von Beton: \( 2,3 \mathrm{~g} / \mathrm{cm}^{3} \) )

Comments

Ich frage mich ebenfalls wie die c) gehen soll. Da muss ich doch das Volumen ausrechnen oder?

---

Ich frage mich ebenfalls wie die c) gehen soll. Da muss ich doch das Volumen ausrechnen oder?

Ja. Die Integralrechnung liefert die Querschnittsfläche. Die Breite ist fest vergegeben. Das langt zur Volumenberechnung.

---

f integrieren von der Schnittstelle mit der x-Achse bis 0, g von 0 bis zur Schnittstelle

Ergebnis mit 6 multiplizieren ( Fläche mal Länge)

Volumen mal 2,3

---

Also ich habe als Querschnittsfläche 25/6 rausbekommen bei der b).

Dann muss ich jetzt 25/6 mal 6 *2.3

Stimmt das so?

---

Querschnittsfläche und Rechenweg sind richtig.

---

Müssen nicht noch die Kubikmeter in Kubikzentimeter umgerechnet werden?

---

Müssen nicht noch die Kubikmeter in Kubikzentimeter umgerechnet werden?

Du kannst vereinfacht auch die Dichte umrechnen:

p = 2.3 g/cm³ = 2.3 kg/dm³ = 2.3 t/m³

---

Oder so....... ;-)

Answer 1

Rechte Rampe: f(x)=a(x-4)². (0|2) einsetzen: 2=a·(-4)², a=1/8

f(x)=1/8(x-4)². Linke Rampe analog.

Comments

Zur rechten Rampe ist gehört die Funktion g

Answer 2

Hallo,

a)es handelt sich dabei um Parabel die an der x-Achse verschoben werden

 allgemein f(x) = a(x+e)²  

   ablesbare Punkte für f , S(-3|0)  und P(0|1,5)

   Funktion f(x) = a(x+3)²

                   1,5  = a(0+3)²     

                    1,5 =  9a          a= 1/6

                   f(x) = 1/6 (x+3)²

bei g   s(4|0) Q (0|2)

                   g(x) = a(x-4)²

                       2= a*16         a=1/8

                    g(x) = 1/8  (x-4)²